Question

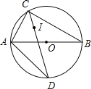
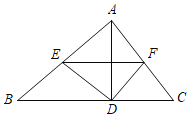
【题目】已知：如图，在△ABC中，∠ACB＝90°，AC＝BC＝4，D是AB的中点，点E是射线CB上的动点，连接DE，DF⊥DE交射线AC于点F．

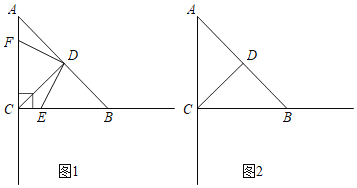
（1）若点E在线段CB上．

①求证：AF＝CE．

②连接EF，试用等式表示AF、EB、EF这三条线段的数量关系，并说明理由．

（2）当EB＝3时，求EF的长．

Answer 1

【答案】（1）①详见解析；②AF2+EB2＝EF2，理由详见解析；（2）或．

【解析】

(1)①证明△ADF≌△CDE(ASA)，即可得出AF=CE；

②由①得△ADF≌△CDE(ASA)，得出AF=CE；同理△CDF≌△BDE(ASA)，得出CF=BE，在Rt△CEF中，由勾股定理得，即可得出结论；

(2)分两种情况：①点E在线段CB上时，求出CE=BC﹣BE=1，由(1)得AF=CE=1，，即可得出答案；

②点E在线段CB延长线上时，求出CE=BC+BE=7，同(1)得△ADF≌△CDE(ASA)，得出AF=CE，求出CF=BE=3，在Rt△EF中，由勾股定理即可得出答案．

(1)①∵△ABC中，∠ACB=90，AC=BC=4，D是AB的中点，

∴∠DCE=45=∠A，CD=AB=AD，CD⊥AB，

∴∠ADC=90，

∵DF⊥DE，

∴∠FDE=90，

∴∠ADC=∠FDE，

∴∠ADF=∠CDE，

在△ADF和△CDE中，，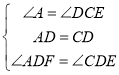

∴△ADF≌△CDE(ASA)，

∴AF=CE；

②，理由如下：

由①得：△ADF≌△CDE(ASA)，

∴AF=CE；

同理：△CDF≌△BDE(ASA)，

∴CF=BE，

在Rt△CEF中，

由勾股定理得：，

∴；

(2)分两种情况：

①点E在线段CB上时，

∵BE=3，BC=4，

∴CE=BC﹣BE=1，

由(1)得：AF=CE=1，，

∴EF；

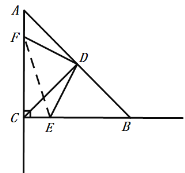
②点E在线段CB延长线上时，如图2所示：

∵BE=3，BC=4，

∴CE=BC+BE=7，

同(1)得：△ADF≌△CDE(ASA)，

∴AF=CE=7，

∴CF=BE=3，

在Rt△CEF中，由勾股定理得：，

∴EF；

综上所述，当EB=3时，EF的长为或．