题目内容
 如图,两圆同心,半径分别为6与8,又矩形ABCD的边AB和CD分别为小大两圆的弦.则当矩形ABCD面积最大时,求此矩形的周长.
如图,两圆同心,半径分别为6与8,又矩形ABCD的边AB和CD分别为小大两圆的弦.则当矩形ABCD面积最大时,求此矩形的周长.
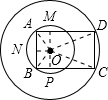 解:作OM⊥AD于点M,ON⊥AB于点N,OP⊥BC于点P.则四边形ANOM是矩形.
解:作OM⊥AD于点M,ON⊥AB于点N,OP⊥BC于点P.则四边形ANOM是矩形.∴S△AOM=S△AON,
同理,S△OBN=S△OPB,
∵ON⊥AB,
∴AN=BN,则OM=OP,
∴△OAM≌△OBP
∴S△AOM=
 S矩形AMPB,
S矩形AMPB,同理,S△OMD=
 S矩形MPCD,
S矩形MPCD,∴S△AOD=
 S矩形ABCD.
S矩形ABCD.又∵S△AOD=
 OA•OD•sin∠AOD=
OA•OD•sin∠AOD= ×6×8sin∠AOD=24sin∠AOD,
×6×8sin∠AOD=24sin∠AOD,当∠AOD=90°时,S△AOD的面积最大,此时矩形ABCD的面积最大.
在直角△AOD中,OA=6,OD=8,
∴AD=
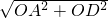 =
= =10,则BC=AD=10.
=10,则BC=AD=10.∵S△AOD=
 AD•OM=
AD•OM= OA•OB,
OA•OB,∴OM=
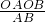 =
=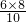 =4.8cm.
=4.8cm.∴AB=CD=2AN=2OM=9.6cm.
则矩形ABCD的周长是:2(9.6+10)=39.2cm.
分析:根据垂径定理可以证明S△AOM=
 S矩形AMPB,然后根据S△AOD=
S矩形AMPB,然后根据S△AOD= OA•OD•sin∠AOD,当∠AOD=90°,矩形的面积最大,即可求得AD的长,AB就是AD的弦心距的2倍,根据直角三角形的面积即可求解,进而求得矩形的周长.
OA•OD•sin∠AOD,当∠AOD=90°,矩形的面积最大,即可求得AD的长,AB就是AD的弦心距的2倍,根据直角三角形的面积即可求解,进而求得矩形的周长.点评:本题主要考查了垂径定理的应用,利用垂径定理可以把求弦长或圆心角的问题转化为解直角三角形的问题.

练习册系列答案
相关题目
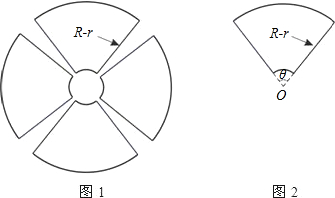 其中R、r分别为大圆和小圆的半径;
其中R、r分别为大圆和小圆的半径; 如图,两圆同心,半径分别为6与8,又矩形ABCD的边AB和CD分别为小大两圆的弦.则当矩形ABCD面积最大时,求此矩形的周长.
如图,两圆同心,半径分别为6与8,又矩形ABCD的边AB和CD分别为小大两圆的弦.则当矩形ABCD面积最大时,求此矩形的周长. 如图所示,两圆同心,半径分别为9cm和5cm,另有一个圆与这两个圆都相切,则此圆的半径为( )
如图所示,两圆同心,半径分别为9cm和5cm,另有一个圆与这两个圆都相切,则此圆的半径为( ) 如图所示,两圆同心,半径分别为9cm和5cm,另有一个圆与这两个圆都相切,则此圆的半径为
如图所示,两圆同心,半径分别为9cm和5cm,另有一个圆与这两个圆都相切,则此圆的半径为