题目内容
如图,矩形OABC中,A(6,0)、C(0,2 )、D(0,3
)、D(0,3 ),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
(1)①点B的坐标是 ;②∠CAO= 度;③当点Q与点A重合时,点P的坐标为 ;(直接写出答案)
(2)设OA的中心为N,PQ与线段AC相交于点M,是否存在点P,使△AMN为等腰三角形?若存在,请直接写出点P的横坐标为m;若不存在,请说明理由.
(3)设点P的横坐标为x,△OPQ与矩形OABC的重叠部分的面积为S,试求S与x的函数关系式和相应的自变量x的取值范围.
解:(1)①(6,2 )。 ②30。③(3,3
)。 ②30。③(3,3 )。
)。
(2)存在。m=0或m=3﹣ 或m=2。
或m=2。
(3)当0≤x≤3时,
如图1,OI=x,IQ=PI•tan60°=3,OQ=OI+IQ=3+x;
由题意可知直线l∥BC∥OA,
可得 ,∴EF=
,∴EF= (3+x),
(3+x),
此时重叠部分是梯形,其面积为:
当3<x≤5时,如图2,

当5<x≤9时,如图3,

当x>9时,如图4,
 。
。
综上所述,S与x的函数关系式为: 。
。
解析

练习册系列答案
相关题目
 如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).
如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5). 17、如图,矩形OABC中,O是原点,OA=8,AB=6,则对角线AC和BO的交点H的坐标为
17、如图,矩形OABC中,O是原点,OA=8,AB=6,则对角线AC和BO的交点H的坐标为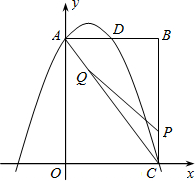

 如图,矩形OABC中,OA=2,OC=1,把矩形OABC放在数轴上,O在原点,OA在正半轴上,把矩形的对角线OB绕着原点O顺时针旋转到数轴上,点B的对应点为B′,则点B′表示的实数是( )
如图,矩形OABC中,OA=2,OC=1,把矩形OABC放在数轴上,O在原点,OA在正半轴上,把矩形的对角线OB绕着原点O顺时针旋转到数轴上,点B的对应点为B′,则点B′表示的实数是( )