题目内容

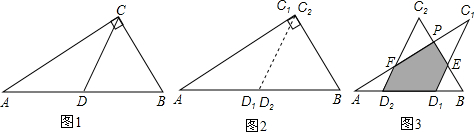
1.如图①,一张三角形ABC纸片,点D、E分别是△ABC边上两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′与∠A的数量关系是__ ▲_________
2.如果折成图②的形状,猜想∠BDA′、∠CEA和∠A的数量关系是__ ▲_________
3.如果折成图③的形状,猜想∠BDA′、∠CEA′和∠A的数量关系,并说明理由.
猜想:▲________
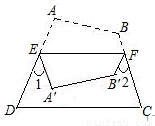
4.将问题1推广,如图,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是_ ▲________
【答案】
1.∠BDA′=2∠A
2.∠BDA′+∠CEA′=2∠A
3.∠BDA-∠CEA=2∠A
4.∠1+∠2=2(∠A+∠B)-360°
【解析】
解:①根据折叠的性质可知∠DA′E=∠A,∠DA′E+∠A=∠BDA′,故∠BDA′=2∠A;
②由图形折叠的性质可知,∠CEA′=180°-2∠DEA′…①,∠BDA′=180°-2∠A′DE…②,
①+②得,∠BDA′+∠CEA′=360°-2(∠DEA′+∠A′DE
即∠BDA′+∠CEA′=360°-2(180°-∠A),
故∠BDA′+∠CEA′=2∠A;
③∠BDA′-∠CEA′=2∠A.
证明如下:
连接AA′构造等腰三角形,
∠BDA′=2∠DA'A,∠CEA'=2∠EA'A,
得∠BDA'-∠CEA'=2∠A,
④由图形折叠的性质可知∠1=180°-2∠AEF,∠2=180°-2∠BFE,
两式相加得,∠1+∠2=360°-2(∠AEF+∠BFE)
即∠1+∠2=360°-2(360°-∠A-∠B),
即∠1+∠2=2(∠A+∠B)-360°.

练习册系列答案
相关题目
 如图,有一张三角形纸片,两直角边BC=6cm,AC=8cm,将△ABC折叠,使点A与点B重合,折痕为DE,求CE的长.
如图,有一张三角形纸片,两直角边BC=6cm,AC=8cm,将△ABC折叠,使点A与点B重合,折痕为DE,求CE的长. 13、亲爱的同学们,在我们的生活中处处有数学的身影,如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理的结论:“三角形的三个内角和等于
13、亲爱的同学们,在我们的生活中处处有数学的身影,如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理的结论:“三角形的三个内角和等于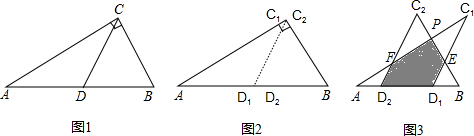
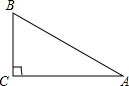 如图,在一张三角形的纸片ABC中,已知∠C=90°,∠A=30°,AB=10.将△ABC纸片折叠后使其中的两个顶点能够互相重合,请画出与说明折痕的各种可能的位置,并求出每条折痕的长.
如图,在一张三角形的纸片ABC中,已知∠C=90°,∠A=30°,AB=10.将△ABC纸片折叠后使其中的两个顶点能够互相重合,请画出与说明折痕的各种可能的位置,并求出每条折痕的长.