题目内容
某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)求销售单价x(元)为多少时,该文具每天的销售利润W(元)最大?
(2)经过试营销后,商场就按(1)中单价销售.为了回馈广大顾客,同时提高该文具知名度,商场营销部决定在11月11日(双十一)当天开展降价促销活动,若每件文具降价m%,则可多售出2m%件文具,结果当天销售额为5250元,求m的值.
(1)求销售单价x(元)为多少时,该文具每天的销售利润W(元)最大?
(2)经过试营销后,商场就按(1)中单价销售.为了回馈广大顾客,同时提高该文具知名度,商场营销部决定在11月11日(双十一)当天开展降价促销活动,若每件文具降价m%,则可多售出2m%件文具,结果当天销售额为5250元,求m的值.
考点:二次函数的应用
专题:
分析:(1)首先确定有关利润与售价x之间的二次函数,配方后即可确定最大利润;
(2)首先确定原来的销售量,然后销售量×单件利润=总利润列出方程求解即可.
(2)首先确定原来的销售量,然后销售量×单件利润=总利润列出方程求解即可.
解答:解:(1)∵销售量=250-10(x-25)=500-10x,
∴总利润=(x-20)(500-10x)
=-10x2+700x-10000
=-10(x-35)2+2250
∴当x=35时,最大利润为2250元.
(2)原来销售量500-10x=500-350=150,
35(1-m%)150(1+2m%)=5250
设m%=a,
∴(1-a)(1+2a)=1,
解得:a=0或a=
,
∵要降价销售,
∴a=
,
∴m=50.
∴总利润=(x-20)(500-10x)
=-10x2+700x-10000
=-10(x-35)2+2250
∴当x=35时,最大利润为2250元.
(2)原来销售量500-10x=500-350=150,
35(1-m%)150(1+2m%)=5250
设m%=a,
∴(1-a)(1+2a)=1,
解得:a=0或a=
| 1 |
| 2 |
∵要降价销售,
∴a=
| 1 |
| 2 |
∴m=50.
点评:本题考查了列一元二次方程解实际问题的运用,一元二次方程的解法的运用,二次函数的性质的运用,解答时根据条件建立方程是解答本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
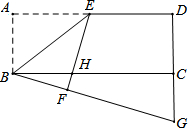 已知如图,在矩形ABCD中,点E是AD的中点,连结BE,将△ABE沿着BE翻折得到△FBE,EF交BC于点H,延长BF、DC相交于点G,若DG=16,BC=24,则FH=
已知如图,在矩形ABCD中,点E是AD的中点,连结BE,将△ABE沿着BE翻折得到△FBE,EF交BC于点H,延长BF、DC相交于点G,若DG=16,BC=24,则FH=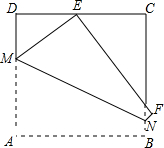 如图,将边长为12cm的正方形ABCD折叠,使得A点落在边CD上的E点,然后压平得折痕MN,若MN的长为13cm,则线段NF的长为
如图,将边长为12cm的正方形ABCD折叠,使得A点落在边CD上的E点,然后压平得折痕MN,若MN的长为13cm,则线段NF的长为 点C在线段AB上,线段AC=6,BC=4,点M,N分别是AC和BC的中点
点C在线段AB上,线段AC=6,BC=4,点M,N分别是AC和BC的中点 如图,一名男生推铅球,铅球进行高度y(m)与水平距离x(m)之间的关系式为:y=-
如图,一名男生推铅球,铅球进行高度y(m)与水平距离x(m)之间的关系式为:y=-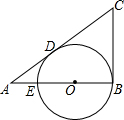 已知,如图,在△ABC中,∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D.若AE=2cm,AD=4cm,则△ABC的面积为( )
已知,如图,在△ABC中,∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D.若AE=2cm,AD=4cm,则△ABC的面积为( )