题目内容
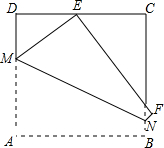 如图,将边长为12cm的正方形ABCD折叠,使得A点落在边CD上的E点,然后压平得折痕MN,若MN的长为13cm,则线段NF的长为
如图,将边长为12cm的正方形ABCD折叠,使得A点落在边CD上的E点,然后压平得折痕MN,若MN的长为13cm,则线段NF的长为考点:翻折变换(折叠问题),正方形的性质
专题:
分析:连结AE,过N点作NG⊥AD于G.根据ASA证明△ADE≌△NGM,可得DE=MG,在Rt△NGM中,根据勾股定理可得MG,设NF=NB=xcm,则NE=NA=(5+x)cm,DM=12-(5+x)=(7-x)cm,在Rt△EDM中,根据勾股定理可得线段NF的长.
解答: 解:连结AE,过N点作NG⊥AD于G.
解:连结AE,过N点作NG⊥AD于G.
由折叠的性质可知,AE⊥MN,
则∠AMN+∠MAE=90°,
∵∠AMN+∠GNM=90°,
∴∠MAE=∠GNM,
在△ADE与△NGM中,
,
∴△ADE≌△NGM(ASA),
∴DE=MG,
在Rt△NGM中,MG=
=
=5cm,
∴DE=5cm,
设NF=NB=xcm,则NE=NA=(5+x)cm,DM=12-(5+x)=(7-x)cm,
在Rt△EDM中,52+(7-x)2=(5+x)2,
解得x=
.
故线段NF的长为
cm.
故答案为:
.
 解:连结AE,过N点作NG⊥AD于G.
解:连结AE,过N点作NG⊥AD于G.由折叠的性质可知,AE⊥MN,
则∠AMN+∠MAE=90°,
∵∠AMN+∠GNM=90°,
∴∠MAE=∠GNM,
在△ADE与△NGM中,
|
∴△ADE≌△NGM(ASA),
∴DE=MG,
在Rt△NGM中,MG=
| MN2-GN2 |
| 132-122 |
∴DE=5cm,
设NF=NB=xcm,则NE=NA=(5+x)cm,DM=12-(5+x)=(7-x)cm,
在Rt△EDM中,52+(7-x)2=(5+x)2,
解得x=
| 49 |
| 24 |
故线段NF的长为
| 49 |
| 24 |
故答案为:
| 49 |
| 24 |
点评:本题考查的是图形翻折变换的性质、三角形全等的判定与性质、勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
下列计算中,正确的是( )
| A、(-1)2×(-1)5=1 | ||||
B、-3÷(-
| ||||
C、
| ||||
| D、-(-3)2=9 |
发射一枚炮弹,经x秒后的高度为y公尺,且时间与高度关系为y=ax2+bx,若此炮弹在第10秒与第20秒时的高度相等,则下列四个时间中,哪一个时间炮弹的高度是最高的?( )
| A、第9秒 | B、第13秒 |
| C、第15秒 | D、第18秒 |
在-3、2、0、-1这四个数中,最小的数是( )
| A、-3 | B、-1 | C、0 | D、2 |
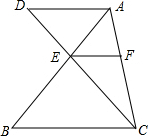 如图所示,在△ABC中,AE:EB=1:2,EF∥BC,AD∥BC交CE的延长线于D,求
如图所示,在△ABC中,AE:EB=1:2,EF∥BC,AD∥BC交CE的延长线于D,求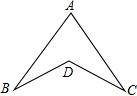 如图,若AB=AC,BD=CD,∠B=20°,∠BDC=120°,则∠A等于
如图,若AB=AC,BD=CD,∠B=20°,∠BDC=120°,则∠A等于