题目内容
19.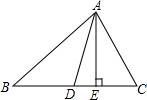 已知AD、AE分别为△ABC的角平分线、高线,若∠B=40°,∠C=60°,则∠ADB的度数为( )
已知AD、AE分别为△ABC的角平分线、高线,若∠B=40°,∠C=60°,则∠ADB的度数为( )| A. | 115° | B. | 110° | C. | 105° | D. | 100° |
分析 根据三角形内角和定理求出∠BAC,根据角平分线定义求出∠BAD,根据三角形内角和定理求出即可.
解答 解:∵∠B=40°,∠C=60°,
∴∠BAC=180°-∠B-∠C=80°,
∵AD、AE分别为△ABC的角平分线、高线,
∴∠BAD=$\frac{1}{2}$∠BAC=40°,
∴∠ADB=180°-∠B-∠BAD=180°-40°-40°=100°,
故选D.
点评 本题考查了三角形内角和定理的应用,能求出∠BAD的度数是解此题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
10.在一条东西走向的街道上,小明先向西走了5米,记作“-5”,又向东走了6米,此时他所在的位置可记作( )
| A. | -11 | B. | -1 | C. | +11 | D. | +1 |
7.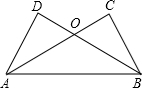 如图,已知AC⊥BC,BD⊥AD,垂足分别为C,D,AC与BD相交于点O,如果AC=BD,那么下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④OC=OD中正确的有( )
如图,已知AC⊥BC,BD⊥AD,垂足分别为C,D,AC与BD相交于点O,如果AC=BD,那么下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④OC=OD中正确的有( )
 如图,已知AC⊥BC,BD⊥AD,垂足分别为C,D,AC与BD相交于点O,如果AC=BD,那么下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④OC=OD中正确的有( )
如图,已知AC⊥BC,BD⊥AD,垂足分别为C,D,AC与BD相交于点O,如果AC=BD,那么下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④OC=OD中正确的有( )| A. | ①②③④ | B. | ①②③ | C. | ①② | D. | ②③ |
14.点P(-2,1)关于x轴对称的点的坐标为( )
| A. | (2,-1) | B. | (-2,1) | C. | (2,1) | D. | (-2,-1) |
4.下列各式从左至右属于因式分解的是( )
| A. | x2-9+8x=(x+3)(x-3)+8x | B. | (x+3)(x-3)+8x=x2-9+8x | ||
| C. | (a+b)(a-b)=a2-b2 | D. | a2-2a(b-c)-3(b-c)2=(a-3b+3c)(a+b-c) |
9.下列四张扑克牌图案中,属于中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
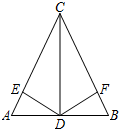 如图,在△ABC中,已知AC=BC,CD平分∠ACB.
如图,在△ABC中,已知AC=BC,CD平分∠ACB.