��Ŀ����
19���۲�����һ������̽�����еĹ��ɣ�-1��$\frac{1}{2}$��-$\frac{1}{3}$��$\frac{1}{4}$��$-\frac{1}{5}$��$\frac{1}{6}$
��1����գ���11��12��13�������ֱ���-$\frac{1}{11}$��$\frac{1}{12}$��-$\frac{1}{13}$��
��2����2015������ʲô����2016���أ�
��3���������������������ȥ�����ĸ���Խ��Խ����
���� ��1����2��ÿһ��ķ��ӷֱ���1����ĸ���ڸ��Ե���ţ����ĸ�ֱ���1��2��3��4��5��6������֪�������Ǹ�����ż��������������n�����ǣ�-1��n$\frac{1}{n}$���ɴ˵ó��𰸼��ɣ�
��3������Ϊ1����ĸԽ��Խ�ӽ�0��
��� �⣺��11��12��13�������ֱ���-$\frac{1}{11}$��$\frac{1}{12}$��-$\frac{1}{13}$��
��2����2015������-$\frac{1}{2015}$����2016����$\frac{1}{2016}$��
��3���������������������ȥ������0Խ��Խ����
���� ���⿼�����ֵı仯���ɣ��ҳ��������еĹ�������ŵ�ȷ�����ó����ɽ�����⣮

��ϰ��ϵ�д�
�����Ŀ
10�����һ�������෴����������������ô������ǣ�������
| A�� | 0 | B�� | 1 | C�� | -1 | D�� | ��1 |
14�� ������a��b�������ϵ�λ����ͼ��ʾ����ô����ʽ���г������ǣ�������
������a��b�������ϵ�λ����ͼ��ʾ����ô����ʽ���г������ǣ�������
 ������a��b�������ϵ�λ����ͼ��ʾ����ô����ʽ���г������ǣ�������
������a��b�������ϵ�λ����ͼ��ʾ����ô����ʽ���г������ǣ�������| A�� | a��0 | B�� | b��0 | C�� | |a|��|b| | D�� | |a|��|b| |
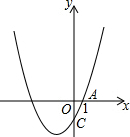 ��ͼ��������y=x2+2x-3��x�������ᣬy��ֱ��ڵ�A��C������P���������ϣ��ҡ�POC������ǡ�AOC�������4�������P�����꣮
��ͼ��������y=x2+2x-3��x�������ᣬy��ֱ��ڵ�A��C������P���������ϣ��ҡ�POC������ǡ�AOC�������4�������P�����꣮