Question

如图（1），在平面直角坐标系中，点A、C分别在y轴和x轴上，AB∥x轴，cosB=

3

5

．点P从B点出发，以1cm/s的速度沿边BA匀速运动，点Q从点A出发，沿线段AO-OC-CB匀速运动．点P与点Q同时出发，其中一点到达终点，另一点也随之停止运动．设点P运动的时间为t（s），△BPQ的面积为S（cm²），已知S与t之间的函数关系如图（2）中的曲线段OE、线段EF与曲线段FG．

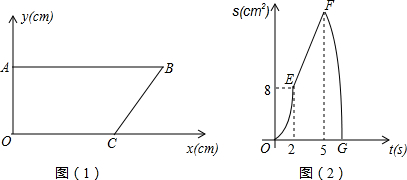
（1）点Q的运动速度为

 

cm/s，点B的坐标为

 

；
（2）求曲线FG段的函数解析式；
（3）当t为何值时，△BPQ的面积是四边形OABC的面积的

1

10

？

Answer 1

考点：动点问题的函数图象

专题：

分析：（1）结合函数图象得出当2秒时，BP=2，此时△BPQ的面积为8cm²，进而求出AO为8cm，即可得出Q点的速度，进而求出AB的长即可；
（2）首先得出PB=t，BQ=30-4t，则QM=

4

5

（30-4t）=24-

16

5

t，利用S_△PBQ=

1

2

t（24-

16

5

t）求出即可；
（3）首先得出△BPQ的面积，进而得出F点坐标，进而得出直线EF解析式为：S=4t，当S=12时，求出t的值，再将S=12代入S=-

8

5

t²+12t求出t的值，即可得出答案．

解答：解：（1）由题意可得出：当2秒时，△BPQ的面积的函数关系式改变，则Q在AO上运动2秒，
当2秒时，BP=2，此时△BPQ的面积为8cm²，
∴AO为8cm，
∴点Q的运动速度为：8÷2=4（cm/s），
当运动到5秒时，函数关系式改变，则CO=12cm，
∵cosB=

3

5

，∴可求出AB=6+12=18（cm），
∴B（18，8）；
故答案为：4，（18，8）；

（2）如图（1）：PB=t，BQ=30-4t，
过点Q作QM⊥AB于点M，
则QM=

4

5

（30-4t）=24-

16

5

t，
∴S_△PBQ=

1

2

t（24-

16

5

t）=-

8

5

t²+12t（5≤t≤7.5），
即曲线FG段的函数解析式为：S=-

8

5

t²+12t；

（3）∵S_梯形OABC=

1

2

（12+18）×8=120，
∴S=

1

10

×120=12，
当t＞2时，F（5，20），
∴直线EF解析式为：S=4t，当S=12时，4t=12，解得：t=3，
将S=12代入S=-

8

5

t²+12t，解得：t=

15± 105

4

，
∵5≤t≤7.5，故t=

15+ 105

4

，
综上所述：t=3或t=

15+ 105

4

，△BPQ的面积是四边形OABC的面积的

1

10

．

点评：此题主要考查了动点问题的函数图象以及三角形，面积求法和待定系数法求函数解析式等知识，利用分类讨论得出是解题关键．