题目内容
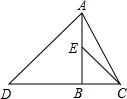如图，AB⊥CD于B，△ABD与△BCE都是等腰直角三角形，若BD=12，AC=13，则△ACE的面积为（ ）| A、30 | B、35 |
| C、17.5 | D、15 |
考点：全等三角形的判定与性质,等腰直角三角形
专题：
分析：易求得AB的长度，在RT△ABC中，根据勾股定理即可求得BC的长度，即可求得AE的长度，即可解题．
解答：解：∵△ABD与△BCE都是等腰直角三角形，
∴AB=BD=12，
∵在RT△ABC中，BC2=AC2-AB2=25，
∴BE=BC=5，
∴AE=AB-AE=7，
∴△ACE的面积=
AE•BC=17.5，
故选 C．
∴AB=BD=12，
∵在RT△ABC中，BC2=AC2-AB2=25，
∴BE=BC=5，
∴AE=AB-AE=7，
∴△ACE的面积=
| 1 |
| 2 |
故选 C．
点评：本题考查了等腰直角三角形的性质，考查了直角三角形中勾股定理的运用，本题中求得AE的长是解题的关键．
练习册系列答案
习题精选系列答案
相关题目
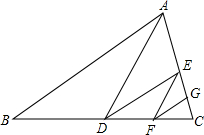如图，AD是△ABC的中线，DE是△ADC的中线，EF是△DEC的中线，FG是△EFC的中线．
如图中，直角三角形中未知边x的长度为：x=已知（a3b-4）2÷（-ab-3）3=3，则a9b3的值是（ ）
| A、-9 | B、9 | C、27 | D、-27 |
下列运算中，正确的是（ ）
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
如图，已知AD是△ABC的中线，且AE：EB=1：6，射线CF交AD于点F，则AF：FD=