题目内容
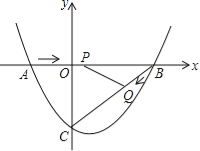
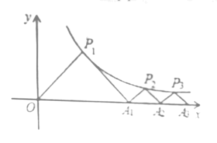
【题目】如图,点![]() ,点
,点![]() ,…点
,…点![]() 在函数
在函数![]() 的图象上,
的图象上, ![]() 都是等腰直角三角形,斜边
都是等腰直角三角形,斜边![]() 都在
都在![]() 轴上(
轴上(![]() 是大于或等于2的正数数),则
是大于或等于2的正数数),则![]() __________.(用含
__________.(用含![]() 的式子表示)
的式子表示)
【答案】![]()
【解析】
过过点P1作P1E⊥x轴于点E,过点P2作P2F⊥x轴于点F,过点P3作P3G⊥x轴于点G,,根据△P1OA1,△P2A1A2,△P3A2A3都是等腰直角三角形,可求出A1,A2,A3的横坐标,从而总结出一般规律得出点An的坐标,再求![]() 的值即可.
的值即可.
解:过点P1作P1E⊥x轴于点E,过点P2作P2F⊥x轴于点F,过点P3作P3G⊥x轴于点G,
∵△P1OA1是等腰直角三角形,
∴P1E=OE=A1E,
设点P1的坐标为(a,a),(a>0),
将点P1(a,a)代入![]() ,可得a=3,
,可得a=3,
故点A1的坐标为(6,0),
设点P2的纵坐标为b,则P2的横坐标为6+b,
将点(b+6,b)代入![]() ,可得b=
,可得b=![]() ,
,
故点A2的横坐标为![]() ,
,
同理可以得到A3的横坐标是![]() ,
,
An的横坐标是![]() ,
,
根据等腰三角形的性质得到![]() An的横坐标的一半,
An的横坐标的一半,
∴![]()
![]() .
.
故答案为:![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目