Question

【题目】平面直角坐标系中，抛物线C1：y1=x2-2mx+2m2-1，抛物线C2：y2=x2-2nx+2n2-1，

（1）若m=2，过点A(0,7)作直线l垂直于y轴交抛物线C1于点B、C两点．

①求BC的长；

②若抛物线C2与直线l交于点E、F两点，若EF长大于BC的长，直接写出n的范围；

（2）若m+n=k(k是常数)，

①若，试说明抛物线C1与抛物线C2的交点始终在定直线上；

②求y1+y2的最小值(用含k的代数式表示) ．

Answer 1

【答案】(1)①4；②-2＜n＜2；(2)①交点横坐标为k，且k是常数，在直线x=k上；②

【解析】

(1)①将m=2代回抛物线C1中，得到解析式，再令解析式中y=7，进而求出B、C两点的横坐标，进而求出BC的长；

②抛物线C2：y2=x2-2nx+2n2-1中令y2=7，求出EF的长为，再利用EF大于BC即可求解；

(2)①联立抛物线C1和C2求出交点的横坐标是常数k，进而确定交点始终在定直线x=k上；

②先算出y1+y2= (x2-2mx+2m2-1)+ (x2-2nx+2n2-1)=2x-2(m+n)x+2(m+n)-2，再将m+n=k整体代入求最值即可.

解：(1)①当m=2时，抛物线C1的解析式为：y1=x2-4x+7，

令y=7，即x2-4x+7=7，解得x1=0，x2=4，

∴BC的长为：4-0=4.

故答案为：4.

②抛物线C2：y2=x2-2nx+2n2-1中令y2=7，

即：x2-2nx+2n2-1=7，解得：x1=，x2=，

∴EF=，

∵EF大于BC，

∴，

解得：，

故答案为：.

(2)①联立抛物线C1和C2

即：，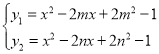

整理有：，

又，∴，等式两边同时除以

∴，

故C1和C2交点的横坐标是常数k，

∴抛物线C1与抛物线C2的交点始终在定直线x=k上.

②由题意知：

y1+y2= (x2-2mx+2m2-1)+ (x2-2nx+2n2-1)

=2x-2(m+n)x+2(m+n)-2

=2x-2kx+2(m+n)-2.

将2x-2kx+2(m+n)-2看成是一个新的函数用y3来表示，

即：y3=2x-2kx+2(m+n)-2，

当其对称轴x=时，y3有最小值，

将x=代入，其最小值为：，

又m+n=k，∴n=m-k，

∴m+n=m+(m-k)=2m-2mk+k，

∴当m=时，此时n=，m+n有最小值为：，

故的最小值为：.

故答案为：.