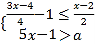Question

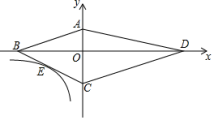
【题目】如图，四边形ABCD的顶点都在坐标轴上，若AB∥CD，AOB与COD面积分别为8和18，若双曲线y＝恰好经过BC的中点E，则k的值为_____．

Answer 1

【答案】6

【解析】

由平行线的性质得∠OAB＝∠OCD，∠OBA＝∠ODC，两个对应角相等证明OAB∽OCD，其性质得，再根据三角形的面积公式，等式的性质求出m＝，线段的中点，反比例函数的性质求出k的值为6．

解：如图所示：

∵AB∥CD，

∴∠OAB＝∠OCD，∠OBA＝∠ODC，

∴OAB∽OCD，

∴，

若＝m，

由OB＝mOD，OA＝mOC，

又∵，，

∴＝，

又∵S△OAB＝8，S△OCD＝18，

∴，

解得：m＝或m＝ (舍去)，

设点A、B的坐标分别为(0，a)，(b，0)，

∵，

∴点C的坐标为(0，﹣a)，

又∵点E是线段BC的中点，

∴点E的坐标为()，

又∵点E在反比例函数上，

∴＝﹣＝，

故答案为：6．