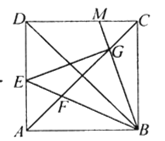
题目内容
【题目】如图，在
中，
为边
的中点．点
从点
出发，以每秒
个单位长度的速度沿
运动到点
停止，同时点
从点出发，以每秒
个单位长度的速度沿折线
运动到点
停止，当点停止运动时，点也停止运动．当点不与的顶点重合时，过点作
交的边于点
以
和
为边作
，设点的运动时间为
(秒)，的面积为
(平方单位)．
（1）当点与点重合时，求的值；
（2）用含的代数式表示的长；
（3）求与之间的函数关系式；
（4）连结
直接写出
将分成面积相等的两部分时的值．
【答案】（1）
；（2）
；（3）
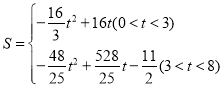；（4）
．
【解析】
（1）先利用勾股定理计算出AC长，在算出动点Q的路径长，再算出时间t；
（2）先分类讨论，分别讨论点Q在边BC上和边CD上，再利用相似三角形的性质表示出
的长；
（3）由（2）得的长，再分类讨论得出所对的高的长度，根据平行四边形的面积公式计算即可；
（4）若
将
分成面积相等的两部分，则有线段PQ的中点E在直线BD上，再将点E的坐标代入直线BD的解析式，解方程即可．
解：（1）
由勾股定理可得：
D为边
的中点
当点
与点
重合时，
（2）当点在边BC上时，
此时，
，即
即
当点在边CD上时，
此时，
，即
即
综上所述：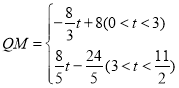
．
（3）当点在边BC上，即时，
由（2）知
当点在边CD上，即时，
由（2）知
，
即
综上所述：
．
（4）以B为坐标原点，AB所在直线为x轴，BC所在直线为y轴，建立如图所致平面直角坐标系，
当点在边BC上时，
由题设条件可知：
，
，
，
易得：PQ中点E的坐标为
直线BD的解析式为
若将分成面积相等的两部分，
则此时点E在直线BD上，
将
代入，得：
解得：
当点在边CD上时，
由题设条件可知：，
，，
易得：PQ中点E的坐标为
直线BD的解析式为
若将分成面积相等的两部分，
则此时点E在直线BD上，
将代入，得：
解得：
【题目】我们把如图1所示的菱形称为基本图形，将此基本图形不断复制并平移，使得相邻两个基本图形的一个顶点与对称中心重合，得到的所有菱形都称为基本图形的特征图形，显然图2中有3个特征图形．
（1）观察以上图形并完成如表：
根据表中规律猜想，图n（n≥2）中特征图形的个数为 ．（用含n的式子表示）
图形名称 | 基本图形的个数 | 特征图形的个数 |
图1 | 1 | 1 |
图2 | 2 | 3 |
图3 | 3 | 7 |
图4 | 4 | |
…… | …… | …… |
（2）若基本图形的面积为2，则图2中小特征图形的面积是 ；图2020中所有特征图形的面积之和为 ．
