题目内容
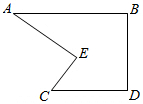 小明到工厂去进行社会实践活动时,发现工人师傅生产了一种如图所示的零件,工人师傅告诉他:AB∥CD,∠BAE=30°,∠AEC=70°,小明马上运用已学的数学知识得出了∠ECD的度数,聪明的你一定知道∠ECD=
小明到工厂去进行社会实践活动时,发现工人师傅生产了一种如图所示的零件,工人师傅告诉他:AB∥CD,∠BAE=30°,∠AEC=70°,小明马上运用已学的数学知识得出了∠ECD的度数,聪明的你一定知道∠ECD=考点:平行线的性质
专题:
分析:延长AE交CD于F,根据平行线的性质求出∠AFC的度数,根据三角形的外角性质求出即可.
解答:解:
延长AE交CD于F,
∵AB∥CD,∠BAE=30°,
∴∠AFC=∠BAE=30°,
∵∠AEC=70°,
∴∠ECD=∠AEC-∠AFC=70°-30°=40°,
故答案为:40°.

延长AE交CD于F,
∵AB∥CD,∠BAE=30°,
∴∠AFC=∠BAE=30°,
∵∠AEC=70°,
∴∠ECD=∠AEC-∠AFC=70°-30°=40°,
故答案为:40°.
点评:本题考查了平行线的性质和三角形的外角性质的应用,解此题的关键是能正确作出辅助线,注意:两直线平行,内错角相等.

练习册系列答案
相关题目
-2015的相反数是( )
A、
| ||
| B、2015 | ||
| C、-2015 | ||
D、-
|
下列图形:①平行四边形;②正方形;③等腰梯形;④菱形;⑤正六边形.其中既是轴对称图形又是中心对称图形的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
某市某天的最高气温为9℃,最低气温为-2℃,则这一天最高气温与最低气温的差为( )
| A、6℃ | B、7℃ | C、9℃ | D、11℃ |
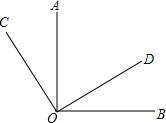 如图:OA⊥OB,OC⊥OD.
如图:OA⊥OB,OC⊥OD. 如图,P是∠AOB的边OB上的一点,
如图,P是∠AOB的边OB上的一点, 如图,在平面直角坐标系中有三点:A(1,0),B(-2,0),C(0,2),点D为y轴上一动点,当四边形ACBD为轴对称图形时,点D的坐标是
如图,在平面直角坐标系中有三点:A(1,0),B(-2,0),C(0,2),点D为y轴上一动点,当四边形ACBD为轴对称图形时,点D的坐标是