题目内容
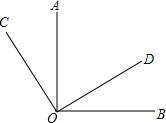 如图:OA⊥OB,OC⊥OD.
如图:OA⊥OB,OC⊥OD.(1)∠AOC、∠BOD相等吗?为什么?
(2)写出∠AOD、∠BOC之间的关系,说明理由.
(3)若∠AOD=
| 4 |
| 5 |
(4)∠AOD和∠BOC的平分线是同一条射线吗,为什么?
考点:余角和补角,垂线
专题:
分析:(1)根据垂线的性质,可得∠AOB=90°,∠COD=90°,根据余角的性质:同角的余角相等,可得答案;
(2)∠AOD+∠BOC=180°,由∠AOB+∠COD=180°,可得∠AOB+∠AOC+∠AOD=180°,即∠BOC+∠AOD=180°;
(3)由(2)的结论:∠AOD+∠BOC=180°,将∠AOD=
∠BOC,代入即可;
(4)∠AOD和∠BOC的平分线是同一条射线.作∠AOD的角平分线OP,然后证明∠COP=∠BOP即可.
(2)∠AOD+∠BOC=180°,由∠AOB+∠COD=180°,可得∠AOB+∠AOC+∠AOD=180°,即∠BOC+∠AOD=180°;
(3)由(2)的结论:∠AOD+∠BOC=180°,将∠AOD=
| 4 |
| 5 |
(4)∠AOD和∠BOC的平分线是同一条射线.作∠AOD的角平分线OP,然后证明∠COP=∠BOP即可.
解答:解:(1)∵OA⊥OB,OC⊥OD,
∴∠AOB=90°,∠COD=90°,
即∠AOC+∠AOD=90°,∠BOD+∠AOD=90°,
∴∠AOC=∠BOD;
(2)∠AOD+∠BOC=180°,
∵∠AOB=90°,∠COD=90°,
∴∠AOB+∠COD=180°,
∴∠AOB+∠AOC+∠AOD=180°,
即∠BOC+∠AOD=180°;
(3)∵∠BOC+∠AOD=180°,∠AOD=
∠BOC,
∴∠BOC+
∠BOC=180°,
∴∠BOC=100°,
∴∠AOD=80°;
(4)作∠AOD的角平分线OP,
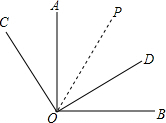
∵OP平分∠AOD,
∴∠AOP=∠DOP,
∵∠COA=∠BOD,
∴∠AOP+∠COA=∠DOP+∠BOD,
即∠COP=∠BOP,
∴OP是∠BOC的平分线,
故∠AOD和∠BOC的平分线是同一条射线.
∴∠AOB=90°,∠COD=90°,
即∠AOC+∠AOD=90°,∠BOD+∠AOD=90°,
∴∠AOC=∠BOD;
(2)∠AOD+∠BOC=180°,
∵∠AOB=90°,∠COD=90°,
∴∠AOB+∠COD=180°,
∴∠AOB+∠AOC+∠AOD=180°,
即∠BOC+∠AOD=180°;
(3)∵∠BOC+∠AOD=180°,∠AOD=
| 4 |
| 5 |
∴∠BOC+
| 4 |
| 5 |
∴∠BOC=100°,
∴∠AOD=80°;
(4)作∠AOD的角平分线OP,

∵OP平分∠AOD,
∴∠AOP=∠DOP,
∵∠COA=∠BOD,
∴∠AOP+∠COA=∠DOP+∠BOD,
即∠COP=∠BOP,
∴OP是∠BOC的平分线,
故∠AOD和∠BOC的平分线是同一条射线.
点评:本题考查了余角和补角,利用余角的性质、垂直的性质、角平分线的性质及角的和差.解题的关键是:熟记这些性质.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
下列各式中与(-a2)3相等的是( )
| A、a5 |
| B、a6 |
| C、-a5 |
| D、-a6 |
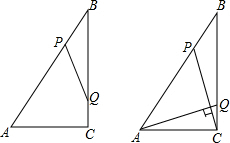 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.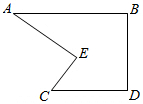 小明到工厂去进行社会实践活动时,发现工人师傅生产了一种如图所示的零件,工人师傅告诉他:AB∥CD,∠BAE=30°,∠AEC=70°,小明马上运用已学的数学知识得出了∠ECD的度数,聪明的你一定知道∠ECD=
小明到工厂去进行社会实践活动时,发现工人师傅生产了一种如图所示的零件,工人师傅告诉他:AB∥CD,∠BAE=30°,∠AEC=70°,小明马上运用已学的数学知识得出了∠ECD的度数,聪明的你一定知道∠ECD= 某个一次函数的图象位置大致如图所示,试分别确定k、b的正负号,并说出函数的性质.
某个一次函数的图象位置大致如图所示,试分别确定k、b的正负号,并说出函数的性质.