题目内容
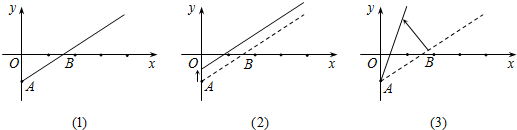
8.若不等式组$\left\{\begin{array}{l}{1+x<a}\\{\frac{x+1}{2}≤\frac{x+2}{3}-1}\end{array}\right.$ 的解是x<a-1,则实数a的取值范围是( )| A. | a≤-6 | B. | a≤-5 | C. | a≤-4 | D. | a<-4 |
分析 先分别解两个不等式得到x<a-1和x≤-5,再根据同小取小可得a-1≤-5,然后解关于a的一元一次不等式即可.
解答 解:$\left\{\begin{array}{l}{1+x<a①}\\{\frac{x+1}{2}≤\frac{x+2}{3}-1②}\end{array}\right.$,
解①得x<a-1,
解②得x≤-5,
而不等式组的解是x<a-1,
所以a-1≤-5,
解得a≤-4.
故选C.
点评 本题考查了解一元一次不等式组:求不等式组的解集的过程叫解不等式组.解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
3.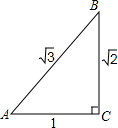 如图,已知Rt△ABC边长分别为1,$\sqrt{2}$,$\sqrt{3}$,则下列三角函数表示正确的是( )
如图,已知Rt△ABC边长分别为1,$\sqrt{2}$,$\sqrt{3}$,则下列三角函数表示正确的是( )
 如图,已知Rt△ABC边长分别为1,$\sqrt{2}$,$\sqrt{3}$,则下列三角函数表示正确的是( )
如图,已知Rt△ABC边长分别为1,$\sqrt{2}$,$\sqrt{3}$,则下列三角函数表示正确的是( )| A. | sinA=$\frac{{\sqrt{3}}}{2}$ | B. | cosA=$\frac{{\sqrt{6}}}{3}$ | C. | tanA=$\sqrt{2}$ | D. | tanA=$\frac{{\sqrt{2}}}{2}$ |
20.下列计算正确的是( )
| A. | a2+a3=a5 | B. | a6÷a3=a2 | C. | (1-a)(1+a)=-a2+1 | D. | 2a2÷(2a2-1)=1-2a2 |
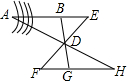 如图所示,要测量AB的长,因为无法过河接近点A,可以作AB外任取一点D,在AB的延长线上任取一点E,连接ED和BD,并且延长BD到G,使DG=BD,延长ED到F,使DF=ED,连接FG,并延长FG到H,使H、D、A在一直线上,则HG=AB,试说明这种测量方法的原理.
如图所示,要测量AB的长,因为无法过河接近点A,可以作AB外任取一点D,在AB的延长线上任取一点E,连接ED和BD,并且延长BD到G,使DG=BD,延长ED到F,使DF=ED,连接FG,并延长FG到H,使H、D、A在一直线上,则HG=AB,试说明这种测量方法的原理.