题目内容
10. 如图,在△ABC中,AB=AC=10,BC=12,点D是AB的中点,点E是AC上一点,且AD=DE,连接BE,则BE的长为9.6.
如图,在△ABC中,AB=AC=10,BC=12,点D是AB的中点,点E是AC上一点,且AD=DE,连接BE,则BE的长为9.6.
分析 首先D是AB的中点,AD=DE,证得△AEB是直角三角形,设AE=x,利用勾股定理求得BE,进一步在△BEC中利用勾股定理建立方程求得x,进一步求得BE即可.
解答 解:∵点D是AB的中点,
∴AD=BD,
∵AD=DE,
∴AD=BD=DE,
∴∠DBE=∠DEB,∠DAE=∠AED,
∴∠AED+∠DEB=$\frac{1}{2}$×180°=90°,
即∠AEB=∠BEC=90°,
设AE=x,
∴BE=$\sqrt{1{0}^{2}-{x}^{2}}$,CE=10-x,
∵BE2+EC2=BC2
∴102-x2+(10-x)2=122
解得:x=2.8,
则BE=$\sqrt{1{0}^{2}-{x}^{2}}$=9.6.
点评 此题考查勾股定理的实际运用,等腰三角形的性质,中点的意义,利用等腰三角形的性质和三角形的内角和求得∠AEB是直角是解决问题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
20.若二元一次方程式组$\left\{\begin{array}{l}{5x-y=5}\\{y=\frac{1}{5}x}\end{array}\right.$的解为x=a,y=b,则a+b等于( )
| A. | $\frac{5}{4}$ | B. | $\frac{75}{13}$ | C. | $\frac{31}{25}$ | D. | $\frac{29}{25}$ |
20.下列计算正确的是( )
| A. | a2+a3=a5 | B. | a6÷a3=a2 | C. | (1-a)(1+a)=-a2+1 | D. | 2a2÷(2a2-1)=1-2a2 |
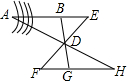 如图所示,要测量AB的长,因为无法过河接近点A,可以作AB外任取一点D,在AB的延长线上任取一点E,连接ED和BD,并且延长BD到G,使DG=BD,延长ED到F,使DF=ED,连接FG,并延长FG到H,使H、D、A在一直线上,则HG=AB,试说明这种测量方法的原理.
如图所示,要测量AB的长,因为无法过河接近点A,可以作AB外任取一点D,在AB的延长线上任取一点E,连接ED和BD,并且延长BD到G,使DG=BD,延长ED到F,使DF=ED,连接FG,并延长FG到H,使H、D、A在一直线上,则HG=AB,试说明这种测量方法的原理. 已知等边△ABC,以AC为腰,在△ABC外作等腰三角形,AD=AC,连接BD,则∠BDC=30°度.
已知等边△ABC,以AC为腰,在△ABC外作等腰三角形,AD=AC,连接BD,则∠BDC=30°度.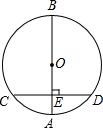 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么线段OE的长为( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么线段OE的长为( )