题目内容
2.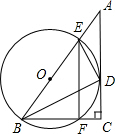 如图:在Rt△ABC中,∠C=90°,BC=9,CA=12,∠ABC的平分线BD交AC于点D,DE垂直DB于点E,点O在AB上,圆O是△BDE的外接圆,交BC于点F,连接EF,求EF:AC的值.
如图:在Rt△ABC中,∠C=90°,BC=9,CA=12,∠ABC的平分线BD交AC于点D,DE垂直DB于点E,点O在AB上,圆O是△BDE的外接圆,交BC于点F,连接EF,求EF:AC的值.
分析 连接OD,先根据勾股定理求出AB的长,再由角平分线的性质得出∠ODB=∠DBC,故OD∥BC.△AOD∽△ABC,由相似三角形的对应边成比例得出r的值,再由圆周角定理得出∠BFE=90°,故EF∥AC,△BEF∽△ABC,再由相似三角形的性质即可得出结论.
解答 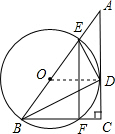 解:连接OD,
解:连接OD,
∵在Rt△ABC中,∠C=90°,BC=9,CA=12,
∴AB=$\sqrt{{AC}^{2}+{BC}^{2}}$=$\sqrt{{12}^{2}+{9}^{2}}$=15.
∵OB=OD,
∴∠OBD=∠ODB.
∵BD平分∠ABC,
∴∠OBD=∠DBC,
∴∠ODB=∠DBC,
∴OD∥BC.
∴△AOD∽△ABC,
∴$\frac{r}{9}$=$\frac{15-r}{15}$,解得r=$\frac{45}{8}$,BE=$\frac{45}{4}$.
∵BE是⊙O的直径,
∴∠BFE=90°,
∴EF∥AC,
∴△BEF∽△ABC,
∴$\frac{EF}{AC}$=$\frac{BE}{AB}$=$\frac{\frac{45}{4}}{15}$=$\frac{3}{4}$.
点评 本题考查的是相似三角形的判定与性质,根据题意作出辅助线,构造出相似三角形是解答此题的关键.

练习册系列答案
相关题目
17.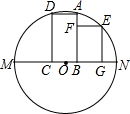 如图,矩形ABCD中,AB=2AD,A、D在半圆O上,B、C在半圆O的直径MN上,另一个矩形BFEG紧靠着矩形ABCD,F在AB上,E在半圆O上,G在直径MN上,且GE=2BG=4,则矩形ABCD的面积为( )
如图,矩形ABCD中,AB=2AD,A、D在半圆O上,B、C在半圆O的直径MN上,另一个矩形BFEG紧靠着矩形ABCD,F在AB上,E在半圆O上,G在直径MN上,且GE=2BG=4,则矩形ABCD的面积为( )
 如图,矩形ABCD中,AB=2AD,A、D在半圆O上,B、C在半圆O的直径MN上,另一个矩形BFEG紧靠着矩形ABCD,F在AB上,E在半圆O上,G在直径MN上,且GE=2BG=4,则矩形ABCD的面积为( )
如图,矩形ABCD中,AB=2AD,A、D在半圆O上,B、C在半圆O的直径MN上,另一个矩形BFEG紧靠着矩形ABCD,F在AB上,E在半圆O上,G在直径MN上,且GE=2BG=4,则矩形ABCD的面积为( )| A. | $\frac{25}{2}$ | B. | 12 | C. | 15 | D. | $\frac{27}{2}$ |
7.已知:a-b=5,c+b=3,则(b+c)-(a-b)的值等于( )
| A. | -2 | B. | 2 | C. | 6 | D. | 8 |
 若将一根长10cm的细木棒放入长、宽、高分别是5cm、4cm、3cm的木箱中,求细木棒露在箱外的最短长度.(精确到0.01cm)
若将一根长10cm的细木棒放入长、宽、高分别是5cm、4cm、3cm的木箱中,求细木棒露在箱外的最短长度.(精确到0.01cm)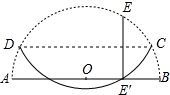 如图,半圆O的半径为2,E是半圆上的一点,将E点对折到直径AB上(EE′⊥AB),当被折的圆弧与直径AB至少有一个交点时,则折痕CD的长度取值范围是2$\sqrt{3}$≤CD<4.
如图,半圆O的半径为2,E是半圆上的一点,将E点对折到直径AB上(EE′⊥AB),当被折的圆弧与直径AB至少有一个交点时,则折痕CD的长度取值范围是2$\sqrt{3}$≤CD<4.