题目内容
20.计算:(1)$\sqrt{18a}-\sqrt{\frac{1}{8}a}+4\sqrt{0.5a}$;
(2)$\sqrt{24}(-\sqrt{\frac{2}{3}}+3\sqrt{\frac{5}{6}}+\sqrt{5})$;
(3)($3\sqrt{3}$+$2\sqrt{2}$)($2\sqrt{3}$-$3\sqrt{2}$)
(4)(4+$\sqrt{5}$)(4-$\sqrt{5}$);
(5)${(3\sqrt{6}-\sqrt{15})^2}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先进行二次根式的乘法运算,然后化简即可;
(3)利用乘法公式展开,然后合并即可;
(4)利用平方差公式计算;
(5)利用完全平方公式计算.
解答 解:(1)原式=3$\sqrt{2a}$-$\frac{\sqrt{2a}}{4}$+2$\sqrt{2a}$
=$\frac{19\sqrt{2a}}{4}$;
(2)原式=-$\sqrt{24×\frac{2}{3}}$+3$\sqrt{24×\frac{5}{6}}$+$\sqrt{24×5}$
=-4+6$\sqrt{5}$+2$\sqrt{30}$;
(3)原式=12-9$\sqrt{6}$+4$\sqrt{6}$-12
=-5$\sqrt{6}$;
(4)原式=16-5
=11;
(5)原式=54-18$\sqrt{10}$+15
=69-18$\sqrt{10}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
9.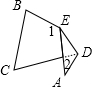 如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )
如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )
 如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )
如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )| A. | ∠1=∠2+∠A | B. | ∠1=2∠A+∠2 | C. | ∠1=2∠2+2∠A | D. | 2∠1=∠2+∠A |
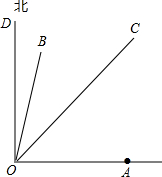 如图,台风中心位于点O处,并沿东北方向(北偏东45°),以40千米/小时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离60$\sqrt{2}$千米的地方有一城市A.
如图,台风中心位于点O处,并沿东北方向(北偏东45°),以40千米/小时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离60$\sqrt{2}$千米的地方有一城市A. 为迎接“六一儿童节”,小天使培训班准备购买“悠悠兔卷笔刀”作为节日礼物送给小朋友.经调查发现:在“丽水沃尔玛超市”悠悠兔卷笔刀的单价为4元/个;在淘宝网店购买,同牌子卷笔刀的价格是超市的8.5折,但需快递费15元.
为迎接“六一儿童节”,小天使培训班准备购买“悠悠兔卷笔刀”作为节日礼物送给小朋友.经调查发现:在“丽水沃尔玛超市”悠悠兔卷笔刀的单价为4元/个;在淘宝网店购买,同牌子卷笔刀的价格是超市的8.5折,但需快递费15元.