题目内容
4.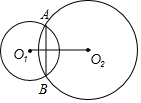 如图,⊙O1与⊙O2相交于A、B两点,⊙O1与⊙O2的半径分别是1和$\sqrt{3}$,O1O2=2,那么两圆公共弦AB的长为$\sqrt{3}$.
如图,⊙O1与⊙O2相交于A、B两点,⊙O1与⊙O2的半径分别是1和$\sqrt{3}$,O1O2=2,那么两圆公共弦AB的长为$\sqrt{3}$.
分析 首先连接O1A,O2A,设AC=x,O1C=y,由勾股定理可得方程组,解方程组即可求得x与y的值,继而求得答案.
解答 解:连接O1A,O2A,如图所示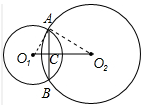
设AC=x,O1C=y,则AB=2AC=2x,
∵O1O2=2,
∴O2C=2-y,
∵AB⊥O1O2,
∴AC2+O1C2=O1A2,O2C2+AC2=O2A2,
∴$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=(\sqrt{3})^{2}}&{\;}\\{{x}^{2}+(2-y)^{2}={1}^{2}}&{\;}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,
∴AC=$\frac{\sqrt{3}}{2}$,
∴AB=2AC=$\sqrt{3}$;
故答案为:$\sqrt{3}$.
点评 此题考查了相交圆的性质与勾股定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
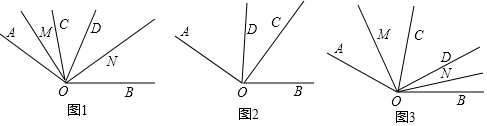

 如图,直线AB与CD相交于点O,∠AOC=$\frac{1}{3}$∠AOD,求∠BOD的度数.
如图,直线AB与CD相交于点O,∠AOC=$\frac{1}{3}$∠AOD,求∠BOD的度数.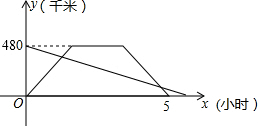 一辆动车和一辆普快分别从A、B两地同时出发相向而行,动车到达B地停留1小时后原速返回A地,结果比普快早1小时到达A地,它们离A地的路程随时间变化的图象如图所示,则下列结论中正确的个数是( )
一辆动车和一辆普快分别从A、B两地同时出发相向而行,动车到达B地停留1小时后原速返回A地,结果比普快早1小时到达A地,它们离A地的路程随时间变化的图象如图所示,则下列结论中正确的个数是( )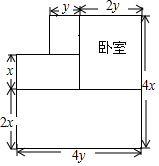 如图,是张老师买的经济适用房平面结构示意图,图中标明了有关尺寸(墙体厚度忽略不计,单位:m),房主计划把卧室以外的地面都铺上地砖,
如图,是张老师买的经济适用房平面结构示意图,图中标明了有关尺寸(墙体厚度忽略不计,单位:m),房主计划把卧室以外的地面都铺上地砖,