题目内容
1.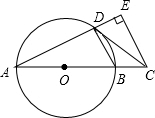 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.(1)求证:∠BDC=∠A;
(2)若CE=2,DE=1,求AD的长.
分析 (1)连接OD,根据圆周角定理得出∠ADB=90°,求出∠A+∠DBO=90°,根据切线的性质求出∠ODC=90°,求出∠BDC+∠ODB=90°,即可得出答案;
(2)求出∠A=∠DCE,根据相似三角形的判定得出△AEC∽△CED,得出比例式,打扰求出即可.
解答 (1)证明: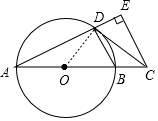
连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A+∠DBO=90°,
∵CD切⊙O于D,
∴∠CDO=90°,
∴∠BDC+∠ODB=90°,
∵OD=OB,
∴∠DBO=∠ODB,
∴∠BDC=∠A;
(2)解:∵CE⊥AE,
∴∠E=∠ADB=90°,
∴DB∥EC,
∴∠DCE=∠BDC,
∵∠BDC=∠A,
∴∠A=∠DCE,
∵∠E=∠E,
∴△AEC∽△CED,
∴$\frac{CE}{DE}$=$\frac{AE}{CE}$,
∴$\frac{2}{1}$=$\frac{AE}{2}$,
∴AE=4,
∴AD=AE-DE=4-1=3.
点评 本题考查了切线的性质,圆周角定理,相似三角形的性质和判定,能灵活运用定理进行推理和计算是解此题的关键.

练习册系列答案
相关题目
11.下列各式能用平方差公式的是( )
| A. | (x-y)(-x+y) | B. | (x-y)(x-y) | C. | (-x-y)(-x+y) | D. | (x+y)(x+y) |
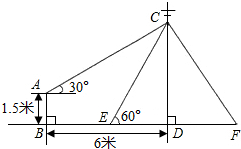 如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).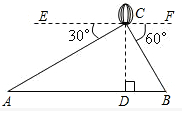 如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60°,如果这时气球的高度CD为120米,且点A、D、B在同一直线上,求建筑物A、B间的距离.(结果保留整数,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60°,如果这时气球的高度CD为120米,且点A、D、B在同一直线上,求建筑物A、B间的距离.(结果保留整数,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( )
如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( )
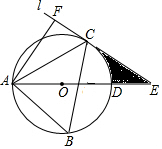 如图,△ABC内接于⊙O,且∠B=60°,过C作⊙O的切线l,与直径AD的延长线交于点E,AF⊥l,垂足为F.
如图,△ABC内接于⊙O,且∠B=60°,过C作⊙O的切线l,与直径AD的延长线交于点E,AF⊥l,垂足为F.