Question

4．如图，直线y=2x+2与直线y=-2x+6交于点P，它们分别与x轴交于A，B．
（1）求点A、B，及两直线的交点P的坐标；
（2）是否存在点Q，使以点A、B、P、Q为顶点的四边形是平行四边形？如果存在，请求出点Q的坐标；如果不存在，请说明理由．

Answer 1

分析 （1）由两函数解析式可求得A、B的坐标，联立两解析式解方程组可求得P点坐标；
（2）当AB为边时，由PQ∥AB且PQ=AB，则容易求得D点坐标；当AB为对角线时，设AB的中点为C，由条件可知PC⊥AB，则可求得PC的长，由平行四边形的性质可求得CQ的长，则可求得Q点的坐标．

解答 解：
（1）在y=2x+2中，令y=0可求得x=-1，在y=-2x+6中，令y=0可求得x=3，
∴A（-1，0），B（3，0），
联立两直线解析式可得$\left\{\begin{array}{l}{y=2x+2}\\{y=-2x+6}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$，
∴P（1，4）；

（2）①当AB为边时，
∵以点A、B、P、Q为顶点的四边形是平行四边形，
∴AB∥PQ，且AB=PQ，
∵P（1，4），
∴Q点纵坐标为4，且PQ=AB=4，
∴Q点坐标为（-3，4）或（5，4）；
②当AB为对角线时，设AB的中点为C，如图，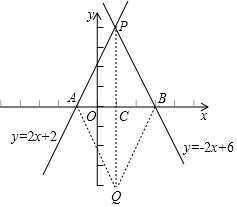

由题意可知PC垂直平分AB，
∴CQ=PC=4，
∴Q（1，-4）；
综上可知Q点的坐标为（-3，4）或（5，4）或（1，-4）．

点评 本题为一次函数的综合应用，涉及函数图象的交点、函数图象与坐标轴的交点、平行四边形的性质及分类讨论思想等知识．在（1）中注意函数图象的交点的求法，在（2）中确定出Q点的位置是解题的关键．本题考查知识点较多，综合性较强，难度适中．