题目内容
1．观察下列各式：13=12，13+23=32，13+23+33=62，13+23+33+43=102，…猜想：13+23+…+n3（n是正整数）=$\frac{{n}^{2}（n+1）^{2}}{4}$．
分析 观察已知等式，得到n个正整数立方和等于各底数之和的平方．
解答 解：根据题意得：13+23+…+n3（n是正整数）=[$\frac{n（n+1）}{2}$]2=$\frac{{n}^{2}（n+1）^{2}}{4}$，
故答案为：$\frac{{n}^{2}（n+1）^{2}}{4}$
点评 此题考查了有理数的混合运算，弄清题中的规律是解本题的关键．
练习册系列答案
相关题目
如图，直线y=2x+2与直线y=-2x+6交于点P，它们分别与x轴交于A，B．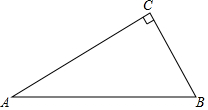
如图，△ABC是直角三角形，∠ACB=90°，∠A=30°