题目内容
如图,AB切⊙O于点A,OD⊥弦AC于点D,延长OD,交AB于点B,若∠O=60°,AC=6cm,则AB= cm.
【答案】分析:由OD⊥弦AC于点D,∠O=60°,AC=6cm,根据垂径定理,可求得AD的长,继而可求得OA的长,又由AB切⊙O于点A,根据切线的性质,即可求得答案.
解答:解:∵OD⊥弦AC,
∴AD= AC=
AC= ×6=3(cm),
×6=3(cm),
∵∠O=60°,
∴OA= =2
=2 (cm),
(cm),
∵AB切⊙O于点A,
∴OA⊥AB,
∴在Rt△OAB中,AB=OA•tan∠O=2 ×
× =6(cm).
=6(cm).
故答案为:6.
点评:此题考查了切线的性质、垂径定理以及三角函数.此题难度适中,注意掌握数形结合思想的应用.
解答:解:∵OD⊥弦AC,
∴AD=
 AC=
AC= ×6=3(cm),
×6=3(cm),∵∠O=60°,
∴OA=
 =2
=2 (cm),
(cm),∵AB切⊙O于点A,
∴OA⊥AB,
∴在Rt△OAB中,AB=OA•tan∠O=2
 ×
× =6(cm).
=6(cm).故答案为:6.
点评:此题考查了切线的性质、垂径定理以及三角函数.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
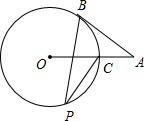 已知:如图,AB切⊙O于点B,OA与⊙O交于点C,点P在⊙O上,若∠BAC=40°,则∠BPC的度数为( )
已知:如图,AB切⊙O于点B,OA与⊙O交于点C,点P在⊙O上,若∠BAC=40°,则∠BPC的度数为( )| A、20° | B、25° | C、30° | D、40° |
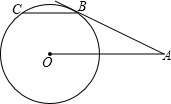 如图,AB切⊙O于点B,OA=2
如图,AB切⊙O于点B,OA=2| 3 |
A、
| ||||
B、
| ||||
| C、π | ||||
D、
|
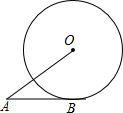 如图,AB切⊙O于点B,AB=4cm,AO=6cm,则⊙O的半径为
如图,AB切⊙O于点B,AB=4cm,AO=6cm,则⊙O的半径为 (2012•西藏)如图,AB切⊙O于点B,延长AO交⊙O于点C,连接BC.若∠A=40°,则∠C=( )
(2012•西藏)如图,AB切⊙O于点B,延长AO交⊙O于点C,连接BC.若∠A=40°,则∠C=( ) (2012•广东模拟)如图,AB切⊙O于点A,OD⊥弦AC于点D,延长OD,交AB于点B,若∠O=60°,AC=6cm,则AB=
(2012•广东模拟)如图,AB切⊙O于点A,OD⊥弦AC于点D,延长OD,交AB于点B,若∠O=60°,AC=6cm,则AB=