题目内容
3. 九个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这九个正方形分成面积相等的两部分,则该直线l的函数关系式是y=-$\frac{9}{11}$x.
九个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这九个正方形分成面积相等的两部分,则该直线l的函数关系式是y=-$\frac{9}{11}$x.
分析 设直线l和九个正方形的最上面交点为A,过A作AB⊥OB于B,B过A作AC⊥OC于C,易知OB=3,利用三角形的面积公式和已知条件求出A的坐标即可得到该直线l的解析式.
解答 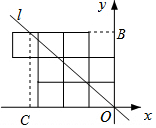 解:设直线l和九个正方形的最上面交点为A,过A作AB⊥OB于B,B过A作AC⊥OC于C,
解:设直线l和九个正方形的最上面交点为A,过A作AB⊥OB于B,B过A作AC⊥OC于C,
∵正方形的边长为1,
∴OB=3,
∵经过原点的一条直线l将这九个正方形分成面积相等的两部分,
∴S△AOB=4.5+1=5.5,
∴$\frac{1}{2}$OB•AB=5.5,
∴AB=$\frac{11}{3}$,
∴OC=$\frac{11}{3}$,
由此可知直线l经过(-$\frac{11}{3}$,3),
设直线方程为y=kx,
则3=-$\frac{11}{3}$k,
k=-$\frac{9}{11}$,
∴直线l解析式为y=-$\frac{9}{11}$x,
故答案为y=-$\frac{9}{11}$x.
点评 此题考查了面积相等问题、用待定系数法求一次函数的解析式以及正方形的性质,此题难度较大,解题的关键是作AB⊥y轴,作AC⊥x轴,根据题意即得到:直角三角形ABO,利用三角形的面积公式求出AB的长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.36÷(-9)的值是( )
| A. | 4 | B. | 18 | C. | -18 | D. | -4 |
12.下列方程是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$=2 | C. | x2+2x=x2-1 | D. | 3(x+1)2=2(x+1) |
8. 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则AE:BC的值等于( )
如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则AE:BC的值等于( )
 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则AE:BC的值等于( )
如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则AE:BC的值等于( )| A. | 1:$\sqrt{2}$ | B. | $\sqrt{2}$:$\sqrt{3}$ | C. | $\sqrt{2}$:2 | D. | 2:3 |
15.已知点A在半径为3的圆上,则点A与圆心O的距离d=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 如图,抛物线y=ax2-8ax(a>0)与x轴交于O,A两点,它的顶点为P,经过O,A两点的圆⊙M与y轴交于点B,抛物线的对称轴与⊙M交于点C,连接AB,BP,当CD:DM:CP=2:3:4时,tan∠ABP的值是$\frac{9}{13}$.
如图,抛物线y=ax2-8ax(a>0)与x轴交于O,A两点,它的顶点为P,经过O,A两点的圆⊙M与y轴交于点B,抛物线的对称轴与⊙M交于点C,连接AB,BP,当CD:DM:CP=2:3:4时,tan∠ABP的值是$\frac{9}{13}$. ,
, )、B(3
)、B(3 ,3
,3 )动点C在X轴上,若以A、B、C三点为顶点的三角形是等腰三角形,则这样的点C有_________个.
)动点C在X轴上,若以A、B、C三点为顶点的三角形是等腰三角形,则这样的点C有_________个.