题目内容
8. 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则AE:BC的值等于( )
如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则AE:BC的值等于( )| A. | 1:$\sqrt{2}$ | B. | $\sqrt{2}$:$\sqrt{3}$ | C. | $\sqrt{2}$:2 | D. | 2:3 |
分析 连接BE,根据圆周角定理得到∠ACB=90°,根据余弦的定义用AB表示出BC,根据弦、弧、圆心角的关系得到AE=BE,根据勾股定理用AB表示出AE,计算即可.
解答 解:连接BE,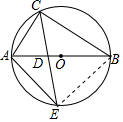
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠B=30°,
∴BC=AB×cosB=$\frac{\sqrt{3}}{2}$AB,
∵CE平分∠ACB,
∴$\widehat{AE}$=$\widehat{BE}$,
∴AE=BE=$\frac{\sqrt{2}}{2}$AB,
∴AE:BC=$\frac{\sqrt{2}}{2}$AB:$\frac{\sqrt{3}}{2}$AB=$\sqrt{2}$:$\sqrt{3}$,
故选:B.
点评 本题考查的是圆周角定理的应用,掌握直径所对的圆周角是直角是解题的关键.

练习册系列答案
相关题目
20.若直角三角形两条直角边的边长分别为 $\sqrt{15}$cm和$\sqrt{12}$cm,那么此直角三角形斜边长是( )
| A. | 3$\sqrt{2}$cm | B. | 3$\sqrt{3}$cm | C. | 9cm | D. | 27cm |
17.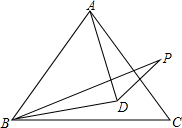 如图所示,在等边△ABC中,BD平分∠PBC,且DB=DA,则∠BPD的度数是( )
如图所示,在等边△ABC中,BD平分∠PBC,且DB=DA,则∠BPD的度数是( )
 如图所示,在等边△ABC中,BD平分∠PBC,且DB=DA,则∠BPD的度数是( )
如图所示,在等边△ABC中,BD平分∠PBC,且DB=DA,则∠BPD的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 无法计算 |
13.小强以5km/h的速度出发,16min后小明从同一地点出发,以13km/h的速度追赶小强,则小明从出发到追上小强所用的时间为( )
| A. | $\frac{1}{6}$h | B. | 10h | C. | $\frac{80}{13}$ | D. | 以上答案都不对 |
 九个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这九个正方形分成面积相等的两部分,则该直线l的函数关系式是y=-$\frac{9}{11}$x.
九个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这九个正方形分成面积相等的两部分,则该直线l的函数关系式是y=-$\frac{9}{11}$x.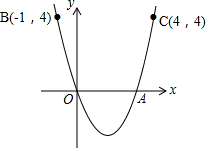 如图,抛物线y=ax2+bx经过原点O,与x轴的另一个交点是A点,点B(-1,4)和点C(4,4)是抛物线上的两个点,则点A的坐标为(3,0).
如图,抛物线y=ax2+bx经过原点O,与x轴的另一个交点是A点,点B(-1,4)和点C(4,4)是抛物线上的两个点,则点A的坐标为(3,0).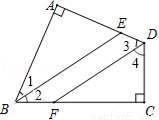
 在实数范围内有意义,则x的取值范围是____________.
在实数范围内有意义,则x的取值范围是____________.