Question

2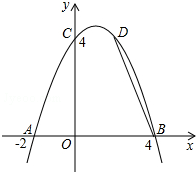．如图，已知抛物线y=ax²+bx+c经过A（-2，0）、B（4，0）、C（0，4）三点．
（1）求此抛物线的解析式；
（2）此抛物线有最大值还是最小值？请求出其最大或最小值．

Answer 1

分析 （1）将A（-2，0）、B（4，0）、C（0，4）代入y=ax²+bx+c，运用待定系数法即可求出此抛物线的解析式；
（2）根据二次项系数，确定抛物线有最大值和最小值即可．

解答 解：（1）将A（-2，0）、B（4，0）、C（0，4）代入y=ax²+bx+c，得
$\left\{\begin{array}{l}{4a-2b+c=0}\\{16a+4b+c=0}\\{c=4}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=1}\\{c=4}\end{array}\right.$．
所以此抛物线的解析式为y=-$\frac{1}{2}$x²+x+4；

（2）∵y=-$\frac{1}{2}$x²+x+4，a=-$\frac{1}{2}$＜0，
∴抛物线有最大值，最大值为$\frac{4×（-\frac{1}{2}）×4-{1}^{2}}{4×（-\frac{1}{2}）}$=$\frac{9}{2}$．

点评 此题考查待定系数法求抛物线的解析式，抛物线的最值的求法，掌握解题的方法与步骤是解决问题的关键．