题目内容
13.三棱柱的三视图如图所示,△EFG中,EF=10cm,EG=16cm,∠EGF=30°,则AB的长为8cm.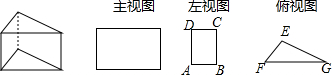
分析 根据三视图的对应情况可得出,△EFG中FG上的高即为AB的长,进而求出即可.
解答  解:过点E作EQ⊥FG于点Q,
解:过点E作EQ⊥FG于点Q,
由题意可得出:EQ=AB,
∵EG=16cm,∠EGF=30°,
∴EQ=AB=$\frac{1}{2}$×16=8(cm).
故答案为:8cm.
点评 此题主要考查了由三视图解决实际问题,根据已知得出EQ=AB是解题关键.

练习册系列答案
相关题目
1.从1,2,3,4,5这五个数字任取两个数字,使其乘积为偶数的概率为( )
| A. | $\frac{4}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
18. 如图,直线a∥b,直线a、b被直线c所截,∠1=40°,则∠2的度数为( )
如图,直线a∥b,直线a、b被直线c所截,∠1=40°,则∠2的度数为( )
 如图,直线a∥b,直线a、b被直线c所截,∠1=40°,则∠2的度数为( )
如图,直线a∥b,直线a、b被直线c所截,∠1=40°,则∠2的度数为( )| A. | 40° | B. | 80° | C. | 140° | D. | 160° |
2. 如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}-|a-b|+\sqrt{{c}^{2}-2ac+{a}^{2}}$可以化简为( )
如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}-|a-b|+\sqrt{{c}^{2}-2ac+{a}^{2}}$可以化简为( )
 如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}-|a-b|+\sqrt{{c}^{2}-2ac+{a}^{2}}$可以化简为( )
如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}-|a-b|+\sqrt{{c}^{2}-2ac+{a}^{2}}$可以化简为( )| A. | -a-b+c | B. | a-b-c | C. | -a-b-c | D. | -a+b-c |
 如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,OP是∠BOC的平分线.
如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,OP是∠BOC的平分线. 如图,反比例函数的图象经过点A(-2,5)和点B(-5,p),?ABCD的顶点C、D分别在y轴的负半轴、x轴的正半轴上,二次函数的图象经过点A、C、D.二次函数的解析式为y=x2-2x-3,若点E在对称轴右侧的二次函数图象上,且∠DCE>∠BDA,则点E的横坐标m的取值范围为1≤m<$\frac{9}{4}$或m>6.
如图,反比例函数的图象经过点A(-2,5)和点B(-5,p),?ABCD的顶点C、D分别在y轴的负半轴、x轴的正半轴上,二次函数的图象经过点A、C、D.二次函数的解析式为y=x2-2x-3,若点E在对称轴右侧的二次函数图象上,且∠DCE>∠BDA,则点E的横坐标m的取值范围为1≤m<$\frac{9}{4}$或m>6.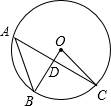 如图,A、B、C三点在圆O上,且OB⊥OC,则∠A的度数是45°.
如图,A、B、C三点在圆O上,且OB⊥OC,则∠A的度数是45°. 几何解释:由图(1)可以看出大正方形的边长是a+b,它是由两个小正方形和两个长方形组成的,所以大正方形的面积等于这四个图形的面积之和.用式子表示为:a2+2ab+b2;观察图(2)利用面积关系可得:(a-b)2+2b(a-b)+b2.
几何解释:由图(1)可以看出大正方形的边长是a+b,它是由两个小正方形和两个长方形组成的,所以大正方形的面积等于这四个图形的面积之和.用式子表示为:a2+2ab+b2;观察图(2)利用面积关系可得:(a-b)2+2b(a-b)+b2.