题目内容
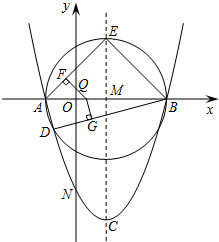
已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,﹣4),与x轴交于A、B两点,与y轴交于点N(0,﹣3).
(1)求这条抛物线的解析式;
(2)如图,以AB为直径作⊙M,与抛物线交于点D,与抛物线的对称轴交于点E,依次连接A、D、B、E,点Q为线段AB上一个动点(Q与A、B两点不重合),过点Q作QF⊥AE于F,QG⊥DB于G,请判断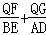 是否为定值?若是,请求出此定值;若不是,请说明理由;
是否为定值?若是,请求出此定值;若不是,请说明理由;
(3)请求出抛物线与(2)中⊙M的所有交点坐标.
解:(1)设抛物线的解析式为y=a(x﹣1)2﹣4,
将N(0,﹣3)代入解析式得:﹣3=a(0﹣1)2﹣4,
∴a=1,
∵抛物线的解析式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3;
(2)是定值: =1,
=1,
理由:∵AB是直径,
∴∠AEB=90°,
∵QF⊥AE,
∴QF∥BE,
∴△AQF∽△ABE,
∴ =
= ,
,
同理: =
= ,
,
∴ =
= =
= =
= =1;
=1;
(3)如图所示,过点D作DN⊥AB,垂足为N.

令y=0得:x2﹣2x﹣3=0,解得:x1=3,x2=﹣1,
∴点A的坐标为(﹣1,0)、点B的坐标为(3,0).
设点D的坐标为(m,m2﹣2m﹣3),
∵AB是直径,
∴∠ADB=90°.
∴∠ADN+∠NDB=90°.
∵∠NDB+∠DBN=90°,
∴∠ADN=∠DBN.
又∵∠AND=∠BND=90°,
∴△ADN∽△DBN.
∴ ,即:
,即:
解得:m1=﹣1(舍去),m2=3(舍去), ,
, .
.
当m=1﹣ 时,m2﹣2m﹣3=
时,m2﹣2m﹣3= =1,
=1,
当m=1+ 时,m2﹣2m﹣3=
时,m2﹣2m﹣3= =1.
=1.
∴点D的坐标为(1﹣ ,﹣1),点D′的坐标为(1+
,﹣1),点D′的坐标为(1+ ,﹣1).
,﹣1).
综上所述,抛物线与圆的交点坐标分别为A(﹣1,0)、B(3,0)、D(1﹣ ,﹣1)、D′(1+
,﹣1)、D′(1+ ,﹣1).
,﹣1).

练习册系列答案
相关题目

 的图象上,则k= .
的图象上,则k= .

 ,0),点B在直线y=x上运动,当线段AB最短时点B的坐为( )
,0),点B在直线y=x上运动,当线段AB最短时点B的坐为( )
 ,﹣
,﹣ ,﹣
,﹣ ) C. (
) C. ( ,
, ) D. (0,0)
) D. (0,0)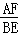 = .
= .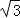 ,求旋转角a的度数.
,求旋转角a的度数.