题目内容
在一次数学活动课上,某校初三数学老师带领学生去测河宽,如图13所示,某学生在河东岸点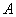 处观测到河对岸水边有一点
处观测到河对岸水边有一点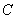 ,测得
,测得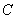 在
在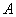 北偏西
北偏西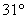 的方向上,沿河岸向北前行20米到达
的方向上,沿河岸向北前行20米到达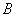 处,测得
处,测得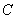 在
在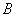 北偏西
北偏西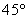 的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈
的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈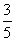 ,sin31°≈
,sin31°≈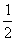 )
) 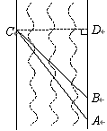
解:过点C作CD⊥AB,垂足为D,设CD=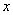 ,在Rt△BCD中,∠CBD=45°
,在Rt△BCD中,∠CBD=45°
∴BD=CD=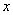 米.…………………………………………………………………………………1分
米.…………………………………………………………………………………1分
在Rt△ACD中,∠DAC=31°,AD=AB+BD=(20+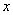 )米,CD=
)米,CD=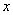 米.…………………………3分
米.…………………………3分
∵ ∠DAC=
∠DAC=
∴ …………………………………………………………………………………5分
…………………………………………………………………………………5分
∴ ………………………………………………………………………………………6分
………………………………………………………………………………………6分
所以这条河宽度约为30米

练习册系列答案
相关题目
某公司有 型产品40件,
型产品40件, 型产品60件,分配给下属甲、乙两
型产品60件,分配给下属甲、乙两 个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
|
|
| |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
(1)设分配给甲店 型产品
型产品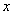 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为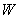 (元),求
(元),求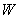 关于
关于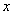 的函数关系式,并求出
的函数关系式,并求出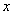 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配 方案,并将
方案,并将 各种方案设计出来;
各种方案设计出来;
(3)为了促销,公司决定仅对甲店 型产品让利销售,每件让利
型产品让利销售,每件让利 元,但让利后
元,但让利后 型产品的每件利润仍高于甲店
型产品的每件利润仍高于甲店 型产品的每件利润.甲店的
型产品的每件利润.甲店的 型产品以及乙店的
型产品以及乙店的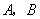 型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?

 与x轴交于An、Bn两点,
与x轴交于An、Bn两点, 表示这两点间的距离,则
表示这两点间的距离,则 的值是
的值是  (B)
(B)
 (D)
(D)
 的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交
的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交 于点M、N,DF
于点M、N,DF AB,垂足为D,AD=1,则重叠部分的面积为 .
AB,垂足为D,AD=1,则重叠部分的面积为 . 
 有一个动点P, PH⊥OA,垂足为H, △PHO的中线PM与NH交于点G.
有一个动点P, PH⊥OA,垂足为H, △PHO的中线PM与NH交于点G.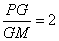 ;
;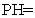
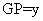 ,求
,求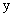 关于
关于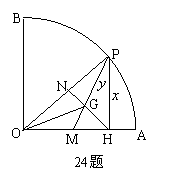
 中自变量x的取值范围是( )
中自变量x的取值范围是( )