Question

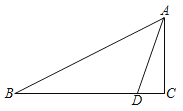
【题目】如图，在Rt△ABC中，∠C＝90°，D是BC边上一点，∠BAD＝45°，AC＝3，AB＝，求BD的长．

Answer 1

【答案】BD的长是5．

【解析】

过D作DE⊥AB于点E，设DE＝a，用a表示出AE、BE，在Rt△ABC和Rt△BDE中分别表示出tan∠ABC，从而列出方程，解方程后即可求出BE、DE的长，然后用勾股定理即可求出BD.

解：过D作DE⊥AB于点E，如图所示，

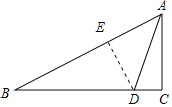
∵∠BAD＝45°，

∴∠EAD＝∠EDA＝45°，

∴AE＝DE，

设DE＝a，则BE＝AB﹣AE＝﹣a，

∵AC＝3，AB＝，∠C＝90°，

∴BC=，

∴，

∴a=，

经检验，a=是上面方程的解.

∴DE=，BE=2

Rt△BED中，由勾股定理得：

BD2＝BE2+DE2=，

∴BD＝5.