题目内容
7. 观察如图所示的几何体,回答下列问题:
观察如图所示的几何体,回答下列问题:(1)填写下表:
| 图形名称 | 底面边数 | 侧面数 | 侧棱数 | 顶点数 | |
| 图① | 三棱柱 | 3 | 3 | 3 | 6 |
| 图② | 四棱柱 | 4 | 4 | 4 | 8 |
| 图③ | 六棱柱 | 6 | 6 | 6 | 12 |
(3)根据(2)中的猜想,直接写出二十棱柱的侧面数、侧棱数、顶点数.
分析 (1)结合三棱柱、四棱柱和五棱柱的特点,即可填表:
(2)根据已知的面、顶点和棱与几棱柱的关系,可知n棱柱一定有(n+2)个面,2n个顶点和3n条棱,进而得出答案;
(3)根据(2)中的猜想,可得二十棱柱的侧面数、侧棱数、顶点数,进而得出答案.
解答 解:(1)填表如下:
| 图形名称 | 底面边数 | 侧面数 | 侧棱数 | 顶点数 | |
| 图① | 三棱柱 | 3 | 3 | 3 | 6 |
| 图② | 四棱柱 | 4 | 4 | 4 | 8 |
| 图③ | 六棱柱 | 6 | 6 | 6 | 12 |
(3)二十棱柱的侧面数是20、侧棱数是20、顶点数是40.
故答案为:3,3,3,6;4,4,4,8;6,6,6,12.
点评 此题主要考查了欧拉公式,熟记常见棱柱的特征,可以总结一般规律:n棱柱有(n+2)个面,2n个顶点和3n条棱是解题关键.

练习册系列答案
相关题目
17.下列说法正确的是( )
| A. | 4的平方根是2 | B. | -4的平方根是-2 | ||
| C. | (-2)2没有平方根 | D. | 2是4的一个平方根 |
12.下列各组代数式,同类项是( )
| A. | 2x与2x2 | B. | -a3与a3 | ||
| C. | -5a2b2与-1.5x2y2 | D. | 4b与3a |
19.下列说法正确的是( )
| A. | 三点确定一个圆 | B. | 长度相等的两条弧是等弧 | ||
| C. | 经过圆内一点有且仅有一条直径 | D. | 半圆是弧 |
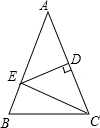 如图,△ABC中,AB=AC,EC=BC,AC的垂直平分线交AB于B,D为垂足,连接EC.
如图,△ABC中,AB=AC,EC=BC,AC的垂直平分线交AB于B,D为垂足,连接EC.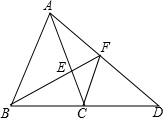 如图,在三角形ABC中,AB=AC,点D在BC延长线上,点E在AC上,连接AD,连接BE并延长,交AD于F,连接FC,已知∠EBC=∠D.
如图,在三角形ABC中,AB=AC,点D在BC延长线上,点E在AC上,连接AD,连接BE并延长,交AD于F,连接FC,已知∠EBC=∠D.