Question

2．如图，梯形OABC中，AB∥OC，BC所在的直线为y=x+12，点A坐标为
A （0，b），其中b＞0，点Q从点C出发经点B到达点A，它在BC上的速度为每秒$\sqrt{2}$个单位，它在AB上的速度为每秒1个单位，点P从点C出发，在线段CO上来回运动，速度为每秒2个单位，当Q到达A点时，P也停止运动． P、Q两点同时从C点出发，运动时间为t秒，过P作直线l垂直于x轴，如图，若以BQ为半径作⊙Q．
（1）当⊙Q第一次和x轴相切时，直接写出t和b的关系式；（用t表示b）
（2）当Q在AB上运动时，若⊙Q和x轴始终没有交点，求b的取值范围；
（3）当b=4时，求直线l与⊙Q从第一次相切到第二次相切经过的时间．

Answer 1

分析 （1）当⊙Q第一次和x轴相切时，设切点为N，作BM⊥x轴，垂足为M，连接QN，用t的代数式表示QC、QB，根据QC=$\sqrt{2}$QB解决问题．
（2）根据AB＜AO，列出关于b的不等式即可解决．
（3）根据题意在点P返回图中与⊙Q相切，此时⊙Q在线段AB上，根据BM+AM=8列出关于t的方程解决．

解答 解：（1）当⊙Q第一次和x轴相切时，设切点为N，作BM⊥x轴，垂足为M，连接QN，
∵AB∥CO，BM∥AO，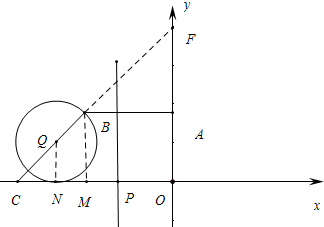
∴四边形AOMB是平行四边形，
∵∠AOM=90°，
∴四边形AOMB是矩形，
∴BM=AO=b，
∵直线BC为y=x+12，
∴C（-12，0），F（0，12），
∴OC=OF，
∴∠BCO=45°，
∵QC=$\sqrt{2}$t，QN⊥CN，
∴QB=QN=t，BC=$\sqrt{2}$b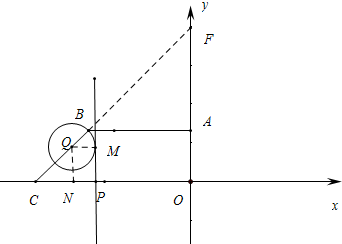
∴$\sqrt{2}$t+t=$\sqrt{2}$b
b=（1+$\frac{\sqrt{2}}{2}$）t．
（2）当AB＜AO时⊙Q与x轴没有交点，即0＜12-b＜b
∴6＜b＜12．
（3）第一次相切时，设切点为M，作QN⊥x轴，连接QM，
∵AO=4，
∴B（-8，4），BC=4$\sqrt{2}$
∵∠QNP=∠NPM=∠QMP=90°，
∴四边形QNPM是矩形，
∴QB=QM=NP=4$\sqrt{2}$-$\sqrt{2}$t，
∵PC=CN+NP，
∴2t=t+4$\sqrt{2}$-$\sqrt{2}$t，
∴t=8-4$\sqrt{2}$，
由题意⊙Q和点P返回途中第二次相遇，如图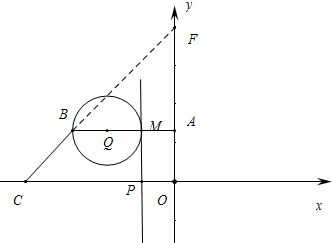，设切点为M，
∵AM=2t-12，BM=2（t-4），AB=8
∴2t-12+2（t-4）=8
∴t=7，
∴直线l与⊙Q从第一次相切到第二次相切经过的时间为7-（8-4$\sqrt{2}$）=（4$\sqrt{2}$-1）秒．

点评 本题考查一次函数、圆、直线与圆相切的判定、等腰梯形、矩形等有关知识，本题综合性比较强，属于运动类问题，根据题意正确画出图形是解题的关键．