题目内容
9. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A,作正方形A2B2C2C1,按这样的规律下去,第2012个正方形的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A,作正方形A2B2C2C1,按这样的规律下去,第2012个正方形的面积为( )| A. | 5•($\frac{3}{2}$)2010 | B. | 5•($\frac{3}{2}$)4022 | C. | 5•($\frac{9}{4}$)2012 | D. | 5•($\frac{9}{4}$)2010 |
分析 与正方形的性质推出AD=AB,∠DAB=∠ABC=∠ABA1=90°=∠DOA,求出∠ADO=∠BAA1,证△DOA∽△ABA1,得出对应边成比例求出AB,BA1,求出边长A1C,求出第二个正方形的面积;同理求出第3个、第4个正方形的面积,得出规律,即可得出结果.
解答 解:∵四边形ABCD,
∴∠DAB=90°,即∠DAO+∠BAA1=90°,
∵∠DAO+∠ADO=90°,
∴∠BAA1=∠AOD,
∵∠AOD=∠A1BA=90°,
∴△AOD∽△A1BA,
∴$\frac{OA}{OD}$=$\frac{{A}_{1}B}{AB}$=$\frac{1}{2}$,
根据OA=1,OD=2,利用勾股定理得:AB=AD=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴A1B=$\frac{1}{2}$AB=$\frac{\sqrt{5}}{2}$,即A1C=A1B+BC=$\frac{3\sqrt{5}}{2}$,
∴第二个正方形A1CC1B1面积为($\frac{3\sqrt{5}}{2}$)2=5•($\frac{3}{2}$)2,
同理得到第三个正方形A2B2C2C1面积为[($\frac{3}{2}$)2×$\sqrt{5}$]2=5•[($\frac{3}{2}$)2]2,
依此类推,第2012个正方形的面积为[($\frac{3}{2}$)2011×$\sqrt{5}$]2=5•($\frac{3}{2}$)4022;
故选:B.
点评 本题考查了正方形的性质,相似三角形的性质和判定,勾股定理的应用,解此题的关键是根据计算的结果得出规律,题目比较好,但是一道比较容易出错的题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.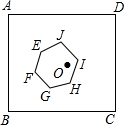 如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )
如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )
 如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )
如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )| A. | $\frac{\sqrt{2}+1}{2}$ | B. | $\frac{\sqrt{2}-1}{2}$ | C. | $\frac{3+2\sqrt{3}}{6}$ | D. | $\frac{3-2\sqrt{3}}{6}$ |
4.已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=3∠A,则此三角形( )
| A. | 一定有一个内角为60° | B. | 一定有一个内角为45° | ||
| C. | 一定是直角三角形 | D. | 一定是钝角三角形 |
14. ,若x=4,则y的值为( )
,若x=4,则y的值为( )
 ,若x=4,则y的值为( )
,若x=4,则y的值为( )| A. | 4 | B. | 10 | C. | 24 | D. | -4 |
1.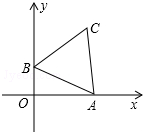 如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )
如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )
 如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )
如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )| A. | $\sqrt{3}-1$ | B. | $\sqrt{3}+1$ | C. | $\sqrt{6}-1$ | D. | $\sqrt{6}+1$ |
19.下列各组式子中,同类项是( )
| A. | 2a2b与3ab2 | B. | -x2y与4yx2 | C. | ax2与bx2 | D. | 3a2与4a3 |
 如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.
如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.