题目内容
4.已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=3∠A,则此三角形( )| A. | 一定有一个内角为60° | B. | 一定有一个内角为45° | ||
| C. | 一定是直角三角形 | D. | 一定是钝角三角形 |
分析 先根据三角形内角和定理,可知∠A+∠B+∠C=180°,即∠B+∠C=180°-∠A,结合已知条件可知3∠A=180°-∠A,解关于∠A的一元一次方程,即可求出∠A.
解答 解:∵∠A+∠B+∠C=180°,
∴∠B+∠C=180°-∠A,
又∵∠B+∠C=3∠A,
∴3∠A=180°-∠A,
∴∠A=45°.
故选B.
点评 本题考查了三角形内角和定理的知识,熟练掌握三角形内角和定理,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
15.下列说法中不正确的是( )
| A. | 直线AB和直线BA是同一条直线 | |
| B. | 平面上两点间的线段的长度叫做这两点的距离 | |
| C. | 四条直线相交最多有六个交点 | |
| D. | 平面上如果AB=BC,则B点是线段AC的中点 |
9. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A,作正方形A2B2C2C1,按这样的规律下去,第2012个正方形的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A,作正方形A2B2C2C1,按这样的规律下去,第2012个正方形的面积为( )
 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A,作正方形A2B2C2C1,按这样的规律下去,第2012个正方形的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A,作正方形A2B2C2C1,按这样的规律下去,第2012个正方形的面积为( )| A. | 5•($\frac{3}{2}$)2010 | B. | 5•($\frac{3}{2}$)4022 | C. | 5•($\frac{9}{4}$)2012 | D. | 5•($\frac{9}{4}$)2010 |
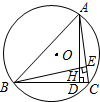 如图,△ABC内接于⊙O,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点H.若BC=6,AH=4,则⊙O的半径为$\sqrt{13}$.
如图,△ABC内接于⊙O,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点H.若BC=6,AH=4,则⊙O的半径为$\sqrt{13}$. 小亮和爸爸上山游玩,小亮乘坐缆车,爸爸步行,两人相约在山顶的缆车终点会合.已知爸爸行走到缆车终点的路程是缆车到山顶的线路长的2倍,小亮在爸爸出发后50分钟才乘上缆车,缆车的平均速度为180米/分钟.设爸爸出发x 分钟后行走的路程为y米.图中的折线表示爸爸在整个行走过程中y随x的变化关系.
小亮和爸爸上山游玩,小亮乘坐缆车,爸爸步行,两人相约在山顶的缆车终点会合.已知爸爸行走到缆车终点的路程是缆车到山顶的线路长的2倍,小亮在爸爸出发后50分钟才乘上缆车,缆车的平均速度为180米/分钟.设爸爸出发x 分钟后行走的路程为y米.图中的折线表示爸爸在整个行走过程中y随x的变化关系. 已知,如图,CD为⊙O的直径,∠EOD=60°,AE交⊙O于点B,E,且AB=OC,求:∠A的度数.
已知,如图,CD为⊙O的直径,∠EOD=60°,AE交⊙O于点B,E,且AB=OC,求:∠A的度数.