题目内容
3.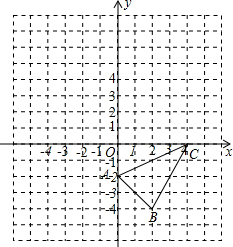 如图,在平面直角坐标系中,每个小正方形的边长为1,请按要求分别完成下列各小题:
如图,在平面直角坐标系中,每个小正方形的边长为1,请按要求分别完成下列各小题:(1)写出△ABC点三个顶点的坐标;
(2)画出△ABC关于x轴对称△A1B1C1,点A1的坐标是(0,2);
(3)画出△ABC关于y轴对称的△A2B2C2;点C2的坐标是(-4,0);
(4)求△ABC的面积.
分析 (1)根据点所在的位置写出点的坐标即可;
(2)先确定出对应点的位置,然后再画出图形即可,根据点A1的位置写出其坐标即可;
(3)先确定出对应点的位置,然后再画出图形即可,根据点C2的位置写出其坐标即可;
(4)利用割补法将三角形的面积转化为一个矩形与三个直角三角形的面积之差即可.
解答 解:(1)A(0,-2),B(2,-4),C(4,0);
(2)如图1所示:
点A1的坐标是(0,2).
故答案为:(0,2).
(3)如图2所示:
点C2的坐标是(-4,0).
故答案为:(-4,0).
(4)如图3所示:
S△ABC=SOCDE-S△AOC-S△CBD-S△ABE
=$4×4-\frac{1}{2}×2×4-\frac{1}{2}×2×4-\frac{1}{2}×2×2$
=6.
点评 本题主要考查的是作图-轴对称变换、点的坐标、三角形的面积,利用割补法求得△ABC的面积是解题的关键.

练习册系列答案
相关题目
13.已知a-b=1,则代数式2a-2b+2013的值是( )
| A. | 2015 | B. | 2014 | C. | 2012 | D. | 2011 |
11.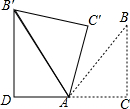 如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )
如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )
 如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )
如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )| A. | 2 | B. | 3 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
15.已知二次函数y=x2-6x+m的最小值是-3,那么m的值等于( )
| A. | 10 | B. | 4 | C. | 5 | D. | 6 |
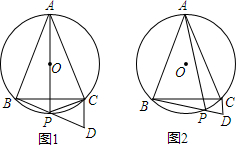
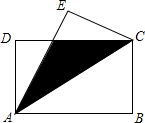 如图,ABCD是长方形,AB=8,BC=6,若将△ABC沿AC对折过来,则B点落到E处,AE交CD于F,求重叠部分的面积.
如图,ABCD是长方形,AB=8,BC=6,若将△ABC沿AC对折过来,则B点落到E处,AE交CD于F,求重叠部分的面积.