题目内容
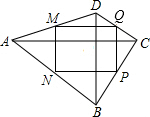 如图,在四边形ABCD中,M、N、P、Q分别是AD、AB、BC、CD的中点,且对角线AC⊥BD,AC:BD=4:3,AC+BD=28,则MQ:QP=
如图,在四边形ABCD中,M、N、P、Q分别是AD、AB、BC、CD的中点,且对角线AC⊥BD,AC:BD=4:3,AC+BD=28,则MQ:QP=考点:中点四边形
专题:
分析:由三角形中位线定理来求MQ:QP的值;有一个角是直角的平行四边形是矩形.利用中位线定理可得出四边形EFGH矩形,根据矩形的面积公式解答即可.
解答:解:①∵AC:BD=4:3,AC+BD=28,
∴AC=16,BD=12.
如图,∵M、Q分别是AD、CD的中点,
∴MQ是△ADC的中位线,
∴MQ=
AC=8.
同理,QP=
BD=6.
∴MQ:QP=8:6=4:3.
故填:4:3;
②∵AC:BD=4:3,AC+BD=28,
∴AC=16,BD=12.
∵点M、N分别为四边形ABCD的边AD、AB的中点,
∴MN∥BD.
同理,PQ∥BD,MQ∥AC,NP∥AC,且
∴MN∥PQ,MQ∥NP,
∴四边形MNPQ是平行四边形.
又∵AC⊥BD,MQ⊥MN,
∴平行四边形MNPQ是矩形.
∴四边形MNPQ的面积是:MQ•PQ=8×6=48,即四边形MNPQ的面积是48.
故填:48.
∴AC=16,BD=12.
如图,∵M、Q分别是AD、CD的中点,
∴MQ是△ADC的中位线,
∴MQ=
| 1 |
| 2 |
同理,QP=
| 1 |
| 2 |
∴MQ:QP=8:6=4:3.
故填:4:3;
②∵AC:BD=4:3,AC+BD=28,
∴AC=16,BD=12.
∵点M、N分别为四边形ABCD的边AD、AB的中点,
∴MN∥BD.
同理,PQ∥BD,MQ∥AC,NP∥AC,且
∴MN∥PQ,MQ∥NP,
∴四边形MNPQ是平行四边形.
又∵AC⊥BD,MQ⊥MN,
∴平行四边形MNPQ是矩形.
∴四边形MNPQ的面积是:MQ•PQ=8×6=48,即四边形MNPQ的面积是48.
故填:48.
点评:本题考查的是中点四边形.解题时,利用了矩形的判定以及矩形的定理,矩形的判定定理有:
(1)有一个角是直角的平行四边形是矩形;
(2)有三个角是直角的四边形是矩形;
(3)对角线互相平分且相等的四边形是矩形.
(1)有一个角是直角的平行四边形是矩形;
(2)有三个角是直角的四边形是矩形;
(3)对角线互相平分且相等的四边形是矩形.

练习册系列答案
相关题目
观察下列图形(每幅图中最小的三角形都是全等的),请写出第n个图中最小的三角形的个数有( )个.


| A、4n |
| B、3n-2 |
| C、n4 |
| D、4n-1 |
 如图,平面直角坐标系,A、B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则A1B1的中点为( )
如图,平面直角坐标系,A、B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则A1B1的中点为( )| A、(1,0.5) |
| B、(2,1) |
| C、(2.5,1.5) |
| D、(2,1.5) |