题目内容
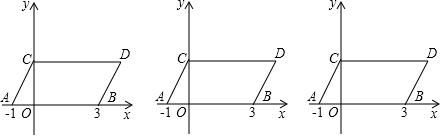
15.直线y=-2x-3与x轴交点坐标为(-$\frac{3}{2}$,0),与y轴的交点坐标为(0,-3),图象经过二、三、四象限.分析 分别根据x、y轴上点的坐标特点及一次函数图象的性质进行解答即可.
解答 解:令y=0,则-2x-3=0,解得x=-$\frac{3}{2}$,故直线与x轴的交点坐标为:(-$\frac{3}{2}$,0);
令x=0,则y=-3,故直线与x轴的交点坐标为:(0,-3);
∵直线y=-2x-3中k=-2<0,b=-3<0,
∴此函数的图象经过二、三、四象限.
故答案为:(-$\frac{3}{2}$,0),(0,-3),二、三、四.
点评 本题考查的是x、y轴上点的坐标特点及一次函数图象的性质,即一次函数y=kx+b(k≠0)中,当k<0,b<0时,函数图象经过二、三、四象限.

练习册系列答案
相关题目
5.一组数据2,6,-4,5,-2,|-4|,2,则这组数据的众数是( )
| A. | 2 | B. | 4 | C. | 6 | D. | -4 |
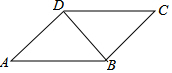 如图,已知?ABCD.
如图,已知?ABCD. 如图,在△ABC中,∠BAC=80°,∠B=35°AD平分∠BAC,则∠ADC的度数为75°.
如图,在△ABC中,∠BAC=80°,∠B=35°AD平分∠BAC,则∠ADC的度数为75°.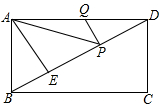 如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为3$\sqrt{3}$.
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为3$\sqrt{3}$.