Question

20．如图，在平面直角坐标系中，点A，B的坐标分别为（-1，0），（3，0），现同时将点A、B分别向上平移2个单位，再向右平移1个单位，分别得到点A、B的对应点C、D，连接AC，BD，CD．
（1）求点C，D的坐标及平行四边形ABDC的面积S_{四边形ABDC}？
（2）若点M是x轴上一个动点，求CM+DM的最小值？
（3）在y轴上是否存在一点P，连接PA，PB，使S_△PAB=2S_{四边形ABDC}，若存在这样一点，求出点P的坐标，若不存在，试说明理由．

Answer 1

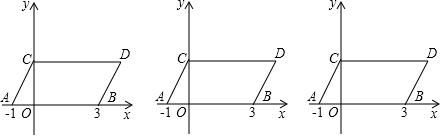
分析 （1）由点A，B的坐标分别为（-1，0），（3，0），现同时将点A、B分别向上平移2个单位，再向右平移1个单位，即可求得点C与D的坐标，继而求得平行四边形ABDC的面积；
（2）首先点C关于x轴的对称点为C′（0，-2），连接C′D，则C′D与x轴的交点即为M，然后由勾股定理求得CM+DM的最小值C′D的长；
（3）由S_△PAB=2S_{四边形ABDC}，可得$\frac{1}{2}$AB×OP=2×8，即可求得答案．

解答 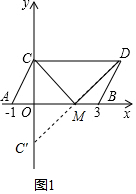解：（1）∵点A，B的坐标分别为（-1，0），（3，0），现同时将点A、B分别向上平移2个单位，再向右平移1个单位，
∴C（0，2），D（4，2），
∴AB=4，OC=2，
∴S_{四边形ABDC}=AB•OC=4×2=8；

（2）如图1，点C关于x轴的对称点为C′（0，-2），连接C′D，则C′D与x轴的交点即为M，
则C′M=CM，CC′=2+2=4，CD=4，
∴CM+DM的最小值=C′M+DM=C′D=$\sqrt{CC{′}^{2}+C{D}^{2}}$=4$\sqrt{2}$；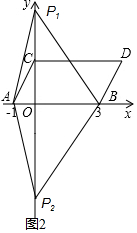

（3）存在．
如图2，∵S_△PAB=2S_{四边形ABDC}，S_{四边形ABDC}=8，
∴$\frac{1}{2}$AB×OP=2×8，
∵AB=4，
∴OP=8，
∴点P的坐标为：（0，8）或（0，-8）．

点评 此题属于四边形的综合题．考查了平行四边形的性质、平移的性质、路径最短问题以及勾股定理等知识．注意分类讨论思想的应用．