题目内容
4.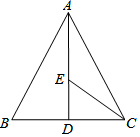 如图所示,在等边三角形ABC中,BC边上的高AD=10,E是AD上一点,现有一动点P沿着折线A-E-C运动,在AE上的速度是4单位/秒,在CE上的速度是2单位/秒,则点P从A到C的运动过程中至少需5秒.
如图所示,在等边三角形ABC中,BC边上的高AD=10,E是AD上一点,现有一动点P沿着折线A-E-C运动,在AE上的速度是4单位/秒,在CE上的速度是2单位/秒,则点P从A到C的运动过程中至少需5秒.
分析 如图,作CH⊥AB于H交AD于E.P沿着折线A-E-C运动的时间=$\frac{EC}{2}$+$\frac{AE}{4}$=$\frac{1}{2}$(EC+$\frac{1}{2}$AE)=$\frac{1}{2}$(EC+EH)=$\frac{1}{2}$CH,根据垂线段最短可知,当CH⊥AB时,P沿着折线A-E-C运动的时间最短,由此即可解决问题.
解答 解:如图,作CH⊥AB于H交AD于E.
∵△ABC是等边三角形,AD⊥BC,
∴∠HAE=30°,∵∠AHE=90°,
∴HE=$\frac{1}{2}$AE,
∵P沿着折线A-E-C运动的时间=$\frac{EC}{2}$+$\frac{AE}{4}$=$\frac{1}{2}$(EC+$\frac{1}{2}$AE)=$\frac{1}{2}$(EC+EH)=$\frac{1}{2}$CH,
根据垂线段最短可知,当CH⊥AB时,P沿着折线A-E-C运动的时间最短,
∵CH、AD是等边三角形的高,
∴CH=AD=10,
∴P沿着折线A-E-C运动的时间最时间=5s.
故答案为5.
点评 本题考查勾股定理、垂线段最短、等边三角形的性质等知识,解题的关键是灵活运用所学知识,用转化的思想思考问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.下列说法:①121的算术平方根是11;②-$\frac{1}{27}$的立方根是-$\frac{1}{3}$;③-81的平方根是±9;④实数和数轴上的点一一对应,其中错误的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
17.如图①,在平面直角坐标系中,平行四边形ABCD在第一象限,且AB∥x轴,直线y=-x从原点出发沿x轴正方向平移,被平行四边形ABCD截得的线段EF的长度l与平移的距离m的函数图象如图②,那么平行四边形ABCD的面积为( )
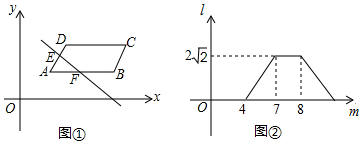

| A. | 4 | B. | $4\sqrt{2}$ | C. | 8 | D. | $8\sqrt{2}$ |
 如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:OE,⑤OD2=DE•CD,正确的有( )
如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:OE,⑤OD2=DE•CD,正确的有( )
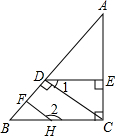 已知,如图,AC⊥BC,HF⊥AB,CD⊥AB,∠1与∠2互补.求证:DE⊥AC.
已知,如图,AC⊥BC,HF⊥AB,CD⊥AB,∠1与∠2互补.求证:DE⊥AC.