题目内容
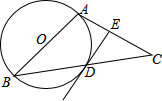 如图,在等腰△ABC中,AB=AC,以AB为直径作⊙O交底边BC于D.
如图,在等腰△ABC中,AB=AC,以AB为直径作⊙O交底边BC于D.(1)求证:BD=CD:
(2)若AB=5,tan∠ABC=
| 3 |
| 4 |
考点:切线的判定,等腰三角形的性质,相似三角形的判定与性质
专题:
分析:(1)连接AD.根据直径所对的圆周角是直角,得到AD⊥BC,再根据等腰三角形三线合一的性质即可证明;
(2)连接OD,根据三角形的中位线定理得到OD∥AC,再证明△ABD∽△DCE,得出∠ADB=∠DEC=90°,根据平行线的性质得到∠ODE=∠DEC=90°,从而证明DE为⊙O的切线.
(2)连接OD,根据三角形的中位线定理得到OD∥AC,再证明△ABD∽△DCE,得出∠ADB=∠DEC=90°,根据平行线的性质得到∠ODE=∠DEC=90°,从而证明DE为⊙O的切线.
解答:(1)证明:连接AD.
∵AB为⊙O的直径,
∴AD⊥BC,
又AB=AC,
∴BD=CD;
 (2)解:DE为⊙O的切线.理由如下:
(2)解:DE为⊙O的切线.理由如下:
连接OD.
∵OA=OB,BD=CD,
∴OD是△ABC的中位线,
∴OD∥AC.
在直角△ABD中,∵∠ADB=90°,AB=5,tan∠ABC=
,
∴AD=3,BD=4.
在△DCE中,DC=4,CE=5-1.8=3.2,
∴
=
=
.
∵AB=AC,
∴∠B=∠C.
在△ABD与△DCE中,
,
∴△ABD∽△DCE,
∴∠ADB=∠DEC=90°,
∵OD∥AC,
∴∠ODE=∠DEC=90°,
∴DE与⊙O相切.
∵AB为⊙O的直径,
∴AD⊥BC,
又AB=AC,
∴BD=CD;
 (2)解:DE为⊙O的切线.理由如下:
(2)解:DE为⊙O的切线.理由如下:连接OD.
∵OA=OB,BD=CD,
∴OD是△ABC的中位线,
∴OD∥AC.
在直角△ABD中,∵∠ADB=90°,AB=5,tan∠ABC=
| 3 |
| 4 |
∴AD=3,BD=4.
在△DCE中,DC=4,CE=5-1.8=3.2,
∴
| AB |
| BD |
| DC |
| CE |
| 5 |
| 4 |
∵AB=AC,
∴∠B=∠C.
在△ABD与△DCE中,
|
∴△ABD∽△DCE,
∴∠ADB=∠DEC=90°,
∵OD∥AC,
∴∠ODE=∠DEC=90°,
∴DE与⊙O相切.
点评:此题综合运用了圆周角定理的推论,即直径所对的圆周角是直角;等腰三角形的性质,即等腰三角形底边上的高也是底边上的中线;三角形的中位线定理以及平行线的性质;切线的判定,即经过半径的外端,且垂直于半径的直线是圆的切线.注意:构造直径所对的圆周角和连接过切点的半径是圆中常见的辅助线之一.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果两个不相等的角的和为180°,则这两个角可能是( )
| A、一个小于直角,一个大于直角 |
| B、两个大于直角的角 |
| C、两个小于直角的角 |
| D、以上答案都不对 |
将抛物线y=x2-4x+5的顶点A向左平移2个单位长度得到点A′,则点A′的坐标是( )
| A、(2,3) |
| B、(2,-1) |
| C、(4,1) |
| D、(0,1) |
 如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若△CDN的面积与△CMN的面积比为1:5,则
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若△CDN的面积与△CMN的面积比为1:5,则 如图,已知一个直角三角形ABC和点O在网格中.
如图,已知一个直角三角形ABC和点O在网格中.