题目内容
 如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若△CDN的面积与△CMN的面积比为1:5,则
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若△CDN的面积与△CMN的面积比为1:5,则| MN |
| BM |
考点:翻折变换(折叠问题)
专题:
分析:首先过点N作NG⊥BC于G,由四边形ABCD是矩形,易得四边形CDNG是矩形,又由折叠的性质,可得四边形AMCN是菱形,由△CDN的面积与△CMN的面积比为1:5,根据等高三角形的面积比等于对应底的比,可得DN:CM=1:5,然后设DN=x,由勾股定理可求得MN的长,继而求得答案.
解答:解:过点N作NG⊥BC于G,如图: ,
,
∵四边形ABCD是矩形,
∴四边形CDNG是矩形,AD∥BC,
∴CD=NG,CG=DN,∠ANM=∠CMN,
由折叠的性质可得:AM=CM,∠AMN=∠CMN,
∴∠ANM=∠AMN,
∴AM=AN,
∴四边形AMCN是平行四边形,
∵AM=CM,
∴四边形AMCN是菱形,
∵△CDN的面积与△CMN的面积比为1:5,
∴DN:CM=1:5,
设DN=x,
则AN=AM=CM=CN=5x,AD=BC=6x,CG=x,
∴BM=x,GM=4x,
在Rt△CGN中,NG=
=
=2
x,
在Rt△MNG中,MN=
=
=2
x,
∴
=
=2
,
故答案为:2
.
 ,
,∵四边形ABCD是矩形,
∴四边形CDNG是矩形,AD∥BC,
∴CD=NG,CG=DN,∠ANM=∠CMN,
由折叠的性质可得:AM=CM,∠AMN=∠CMN,
∴∠ANM=∠AMN,
∴AM=AN,
∴四边形AMCN是平行四边形,
∵AM=CM,
∴四边形AMCN是菱形,
∵△CDN的面积与△CMN的面积比为1:5,
∴DN:CM=1:5,
设DN=x,
则AN=AM=CM=CN=5x,AD=BC=6x,CG=x,
∴BM=x,GM=4x,
在Rt△CGN中,NG=
| CN2-CG2 |
| (5x)2-x2 |
| 6 |
在Rt△MNG中,MN=
| GM2+NG2 |
(4x)2+(2
|
| 10 |
∴
| MN |
| BM |
2
| ||
| x |
| 10 |
故答案为:2
| 10 |
点评:此题考查了翻折变换,利用了折叠的性质、矩形的判定与性质、菱形的判定与性质以及勾股定理.此题难度较大,注意掌握辅助线的作法,注意折叠中的对应关系,注意数形结合与方程思想的应用.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
分式方程
=
的解为( )
| 2 |
| x-1 |
| 3 |
| x |
| A、x=-3 | B、x=-1 |
| C、x=1 | D、x=3 |
 如图:点M是Rt△ABC的斜边BC上不与B、C重合的一定点,过点M作直线截△ABC,使截得的三角形与原△ABC相似,这样的直线共有
如图:点M是Rt△ABC的斜边BC上不与B、C重合的一定点,过点M作直线截△ABC,使截得的三角形与原△ABC相似,这样的直线共有 如图,点A、B、C为⊙O上的三点,连接AC,若∠OCA=40°,则∠ABC的度数为
如图,点A、B、C为⊙O上的三点,连接AC,若∠OCA=40°,则∠ABC的度数为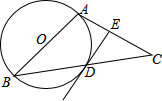 如图,在等腰△ABC中,AB=AC,以AB为直径作⊙O交底边BC于D.
如图,在等腰△ABC中,AB=AC,以AB为直径作⊙O交底边BC于D.