题目内容
2.(1)解不等式组:$\left\{\begin{array}{l}{2(x-3)+x≤3}\\{\frac{x+5}{3}<\frac{x}{2}+2}\end{array}\right.$,写出使不等式组成立的所有整数x.(2)解方程:$\frac{2}{x-1}-\frac{3}{x+1}=1$.
分析 (1)分别求出各不等式的解集,再求出其公共解集,在其公共解集内找出使不等式组成立的所有整数x即可;
(2)先去分母,把分式方程化为整式方程,求出x的值,再代入最简公分母进行检验即可.
解答 解:(1)$\left\{\begin{array}{l}2(x-3)+x≤3①\\ \frac{x+5}{3}<\frac{x}{2}+2②\end{array}\right.$,由①得,x≤3,由②得,x>-2,
故不等式组的解集为:-2<x≤3,使不等式组成立的所有整数是:-1,0,1,2,3;
(2)方程两边同时乘以(x+1)(x-1)得,2(x+1)-3(x-1)=(x+1)(x-1),
化简得,x2+x-6=0,解得x1=3,x2=2,
经检验,x1=3,x2=2均是原分式方程的解.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
12.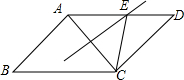 如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )
如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )
 如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )
如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )| A. | 6 | B. | 8 | C. | 14 | D. | 16 |
13.方程x2-4x+4=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 只有一个实数根 | ||
| C. | 没有实数根 | D. | 有两个不相等的实数根 |
10.某班45名同学举行的“爱心涌动校园”募捐活动中捐款情况如下表所示
则该班捐款的平均数为24元.
| 捐款数(元) | 10 | 20 | 30 | 40 | 50 |
| 捐款人数(人) | 8 | 17 | 16 | 2 | 2 |