题目内容
已知,关于x的二次三项式mx2-(2m-1)x+m+1.
(1)当m为何值时,这个二次三项式在实数范围内能因式分解?
(2)当m为何值时,这个二次三项式在实数范围内能因式分解成一个完全平方式?并请将这个完全平方式进行因式分解.应改成“二次三项式”
(1)当m为何值时,这个二次三项式在实数范围内能因式分解?
(2)当m为何值时,这个二次三项式在实数范围内能因式分解成一个完全平方式?并请将这个完全平方式进行因式分解.应改成“二次三项式”
考点:实数范围内分解因式,完全平方式
专题:
分析:(1)根据十字相乘法,可分解因式,可得答案;
(2)根据完全平方公式:和的平方根等于平方和加积的二倍,差的平方等于平方和减积的二倍,可得答案.
(2)根据完全平方公式:和的平方根等于平方和加积的二倍,差的平方等于平方和减积的二倍,可得答案.
解答:解(1)mx2-(2m-1)x+m+1-[mx-(m+1)][x-1],得m≠0,
当m≠0时,关于x的二次三项式mx2-(2m-1)x+m+1;
(2)mx2-(2m-1)x+m+1=[
x-
]2,得2
×
=2m-1,
平方,得4m2+4m=4m2-4m+1.
解得m=
,
当m=
时,这个二次三项式在实数范围内能因式分解成一个完全平方式,
mx2-(2m-1)x+m+1=
x2+
x+
.
当m≠0时,关于x的二次三项式mx2-(2m-1)x+m+1;
(2)mx2-(2m-1)x+m+1=[
| m |
| m+1 |
| m |
| m+1 |
平方,得4m2+4m=4m2-4m+1.
解得m=
| 1 |
| 8 |
当m=
| 1 |
| 8 |
mx2-(2m-1)x+m+1=
| 1 |
| 8 |
| 3 |
| 4 |
| 9 |
| 8 |
点评:本题考查了实数范围内分解因式,(1)利用了十字相乘法;(2)利用了差的平方等平方和减积的二倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
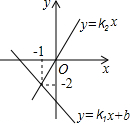 同一平面直角坐标系中,一次函数y=k1x+b的图象与一次函数y=k2x的图象如图所示,则关于x的方程k1x+b=k2x的解为( )
同一平面直角坐标系中,一次函数y=k1x+b的图象与一次函数y=k2x的图象如图所示,则关于x的方程k1x+b=k2x的解为( )| A、x=0 | B、x=-1 |
| C、x=-2 | D、x=1 |
计算:a÷
•b•c÷
÷
•d=( )
| 1 |
| b |
| 1 |
| c |
| 1 |
| d |
| A、a | ||
B、
| ||
C、
| ||
| D、ab2c2d |
 如图所示,点M,N在线段AB上,且MB=5cm,NB=14cm,N是线段AM的中点,则线段AB为
如图所示,点M,N在线段AB上,且MB=5cm,NB=14cm,N是线段AM的中点,则线段AB为 如图,在△ABC中,AD是BC边上的高,AC=3
如图,在△ABC中,AD是BC边上的高,AC=3