题目内容
在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2-3向右平移1个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.
(1)求点M、A、B坐标;
(2)若顶点为M的抛物线与x轴的两个交点为D、C,试求线段DC的长.
(1)求点M、A、B坐标;
(2)若顶点为M的抛物线与x轴的两个交点为D、C,试求线段DC的长.
考点:二次函数图象与几何变换,抛物线与x轴的交点
专题:
分析:(1)抛物线y=x2-3的顶点坐标为(0,-3),顶点向右平移一个单位后得到M点的坐标为(1,-3),所以平移后的抛物线解析式为y=(x-1)2-3;再求x=0的函数值即可得到A点坐标;然后求自变量为3时的函数值即可得到B点坐标;
(2)根据抛物线与x轴的交点问题,解方程(x-1)2-3=0即可得到C、D的坐标,然后计算两点之间的距离即可.
(2)根据抛物线与x轴的交点问题,解方程(x-1)2-3=0即可得到C、D的坐标,然后计算两点之间的距离即可.
解答:解:(1)抛物线y=x2-3向右平移一个单位后得到的函数解析式为y=(x-1)2-3,则顶点M的坐标为(1,-3),
令x=0,则y=(0-1)2-3=-2,则点A的坐标为(0,-2),
当x=3时,y=(3-1)2-3=4-3=1,则点B坐标为(3,1);
(2)令y=0,则(x-1)2-3=0,解得x1=
+1,x2=-
-1,则D(
+1,0),C(
-1,0),
所以DC=2
.
令x=0,则y=(0-1)2-3=-2,则点A的坐标为(0,-2),
当x=3时,y=(3-1)2-3=4-3=1,则点B坐标为(3,1);
(2)令y=0,则(x-1)2-3=0,解得x1=
| 3 |
| 3 |
| 3 |
| 3 |
所以DC=2
| 3 |
点评:本题考查了二次函数与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
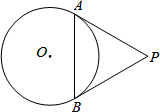 如图,PA,PB分别与⊙O相切于点A,B,连接AB.∠APB=60°,AB=5,则PA的长是
如图,PA,PB分别与⊙O相切于点A,B,连接AB.∠APB=60°,AB=5,则PA的长是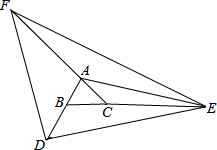 如图,延长等边△ABC的边AB到D,使BD=3,延长BC到E,使CE=4,延长CA到F,使AF=5,若△DEF的面积为
如图,延长等边△ABC的边AB到D,使BD=3,延长BC到E,使CE=4,延长CA到F,使AF=5,若△DEF的面积为 如图,已知AB⊥BD,CD⊥BD,点E、F在BC上,AF,CE相交于点O,AF=CE,BE=DF,求证:
如图,已知AB⊥BD,CD⊥BD,点E、F在BC上,AF,CE相交于点O,AF=CE,BE=DF,求证: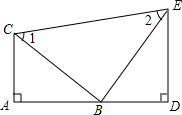 已知:如图,A,B,D在同一条直线上,∠1=∠2,∠A=∠D=Rt∠,AC=BD.
已知:如图,A,B,D在同一条直线上,∠1=∠2,∠A=∠D=Rt∠,AC=BD.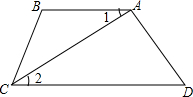 根据下列证明过程填空:如图,已知AB∥CD,∠B=120°,CA平分∠BCD,求证:∠1=30°
根据下列证明过程填空:如图,已知AB∥CD,∠B=120°,CA平分∠BCD,求证:∠1=30°