题目内容
13.当x>$\frac{5}{2}$时,分式$\frac{2x-5}{{x}^{2}+5}$的值为正.分析 若要使分式$\frac{2x-5}{{x}^{2}+5}$的值为正,则分子分母的符号相同,得出2x-5>0,通过解不等式得到x>$\frac{5}{2}$.
解答 解:∵$\frac{2x-5}{{x}^{2}+5}$>,
∵x2+5>0,
∴2x-5>0,
∴x>$\frac{5}{2}$.
故答案为:>$\frac{5}{2}$.
点评 本题考查分式值的正负性问题,若对于分式$\frac{a}{b}$(b≠0)>0时,说明分子分母同号;分式$\frac{a}{b}$(b≠0)<0时,分子分母异号.

练习册系列答案
相关题目
3.在表中,记录了一个同学10次练习立定跳远的成绩:
y是x的函数吗?为什么?
| 练习跳远次数x/次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 跳远成绩y/米 | 2.3 | 2.35 | 2.42 | 2.4 | 2.55 | 2.4 | 2.5 | 2.45 | 2.6 | 2.48 |
 如图所示,M、N分别是AB、CD的中点,MN=a,BC=b,求AD的长.
如图所示,M、N分别是AB、CD的中点,MN=a,BC=b,求AD的长.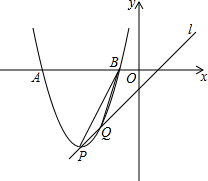 已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.
已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.