题目内容
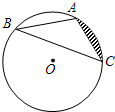（2012•丰润区二模）如图，已知：△ABC是⊙O的内接三角形，∠B=30°，若AC=6，则图中阴影部分的面积是（ ）分析：根据等边三角形的判定得出△AOC是等边三角形，进而得出等边三角形的面积，再利用扇形AOC的面积公式，即可得出图中阴影部分的面积．
解答：
解：连接AO，CO，过点O作ON⊥AC于点N，
∵△ABC是⊙O的内接三角形，∠B=30°，
∴∠AOC=60°，
∵AO=CO，
∴△AOC是等边三角形，
∵AC=6，ON⊥AC，
∴AN=NC=3，
∴ON=
=3
，
∴△AOC的面积为：
×6×3
=9
，
扇形AOC的面积为：
=6π，
∴图中阴影部分的面积是：6π-9
．
故选：B．
解：连接AO，CO，过点O作ON⊥AC于点N，∵△ABC是⊙O的内接三角形，∠B=30°，
∴∠AOC=60°，
∵AO=CO，
∴△AOC是等边三角形，
∵AC=6，ON⊥AC，
∴AN=NC=3，
∴ON=
| 62-32 |
| 3 |
∴△AOC的面积为：
| 1 |
| 2 |
| 3 |
| 3 |
扇形AOC的面积为：
| 60×π×62 |
| 360 |
∴图中阴影部分的面积是：6π-9
| 3 |
故选：B．
点评：此题主要考查了等边三角形的判定和扇形面积求法和等边三角形面积求法等知识，根据已知得出等边三角形的高是解题关键．
练习册系列答案
相关题目
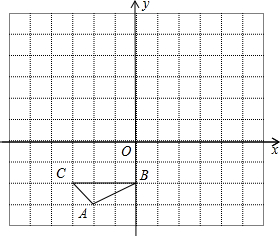（2012•丰润区二模）如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，△ABC的顶点都在格点上，建立平面直角坐标系．
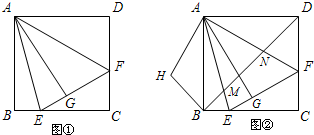（2012•丰润区二模）如图①，在正方形ABCD中，△AEF的顶点E、F分别在BC、CD边上，高AG与正方形的边长相等．