题目内容
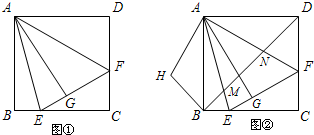 (2012•丰润区二模)如图①,在正方形ABCD中,△AEF的顶点E、F分别在BC、CD边上,高AG与正方形的边长相等.
(2012•丰润区二模)如图①,在正方形ABCD中,△AEF的顶点E、F分别在BC、CD边上,高AG与正方形的边长相等.(1)求∠EAF的度数;
(2)在图①中,连接BD分别交AE、AF于点M、N,将△ADN绕点A顺时针旋转90°至△ABH位置,得到图②.求证:MN2=MB2+ND2;
(3)在图②中,若BE=4,DF=6,BM=3
| 2 |
分析:(1)根据正方形的性质和全等三角形的判定方法证明Rt△ABE≌Rt△AGE和Rt△ADF≌Rt△AGF,由全等三角形的性质即可求出∠EAF=
∠BAD=45°;
(2)连接MH,由旋转知:∠BAH=∠DAN,AH=AN,由旋转知:∠ABH=∠ADB=45°,HB=ND,所以∠HBM=∠ABH+∠ABD=90°,所以MH2=HB2+ND2,所以MN2=MB2+ND2;
(3)由(1)知,Rt△ABE≌Rt△AGE,Rt△ADF≌Rt△AGF,设AG=x,则CE=x-4,CF=x-6.因为CE2+CF2=EF2,所以(x-4)2+(x-6)2=102.解这个方程,求出x的值即可得到AG=12,在(2)中,MN2=MB2+ND2,MN=a,则a2=(3
)2+(12
-3
-a)2,所以a=5
.即MN=5
.
| 1 |
| 2 |
(2)连接MH,由旋转知:∠BAH=∠DAN,AH=AN,由旋转知:∠ABH=∠ADB=45°,HB=ND,所以∠HBM=∠ABH+∠ABD=90°,所以MH2=HB2+ND2,所以MN2=MB2+ND2;
(3)由(1)知,Rt△ABE≌Rt△AGE,Rt△ADF≌Rt△AGF,设AG=x,则CE=x-4,CF=x-6.因为CE2+CF2=EF2,所以(x-4)2+(x-6)2=102.解这个方程,求出x的值即可得到AG=12,在(2)中,MN2=MB2+ND2,MN=a,则a2=(3
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
解答:解:(1)在Rt△ABE和Rt△AGE中,AB=AG,AE=AE,
∴Rt△ABE≌Rt△AGE,
∴∠BAE=∠GAE.
同理,Rt△ADF≌Rt△AGF,
∴∠GAF=∠DAF.
∵四边形ABCD是正方形,
∴∠BAD=90°
∴∠EAF=
∠BAD=45°;
(2)证明:连接MH,
由旋转知:∠BAH=∠DAN,AH=AN,
∵四边形ABCD是正方形,∴∠BAD=90°,∵∠EAF=45°,
∴∠BAM+∠DAN=45°,∴∠HAM=∠BAM+∠BAH=45°,
∴∠HAM=∠NAM,又AM=AM,
∴△AHM≌△ANM,
∴MN=MH
∵四边形ABCD是正方形,
∴∠ADB=∠ABD=45°
由旋转知:∠ABH=∠ADB=45°,HB=ND,
∴∠HBM=∠ABH+∠ABD=90°,
∴MH2=HB2+ND2,
∴MN2=MB2+ND2;
(3)由(1)知,Rt△ABE≌Rt△AGE,Rt△ADF≌Rt△AGF,
∴BE=EG=4,DF=FG=6,则EF=10
设AG=x,则CE=x-4,CF=x-6.
∵CE2+CF2=EF2,
∴(x-4)2+(x-6)2=102.
解这个方程,得x1=12,x2=-2(舍去).
∴AG=12.(9分)
∴BD=
=
=12
.
在(2)中,MN2=MB2+ND2
设MN=a,则a2=(3
)2+(12
-3
-a)2.
∴a=5
.即MN=5
.
∴Rt△ABE≌Rt△AGE,
∴∠BAE=∠GAE.
同理,Rt△ADF≌Rt△AGF,
∴∠GAF=∠DAF.
∵四边形ABCD是正方形,
∴∠BAD=90°

∴∠EAF=
| 1 |
| 2 |
(2)证明:连接MH,
由旋转知:∠BAH=∠DAN,AH=AN,
∵四边形ABCD是正方形,∴∠BAD=90°,∵∠EAF=45°,
∴∠BAM+∠DAN=45°,∴∠HAM=∠BAM+∠BAH=45°,
∴∠HAM=∠NAM,又AM=AM,
∴△AHM≌△ANM,
∴MN=MH
∵四边形ABCD是正方形,
∴∠ADB=∠ABD=45°
由旋转知:∠ABH=∠ADB=45°,HB=ND,
∴∠HBM=∠ABH+∠ABD=90°,
∴MH2=HB2+ND2,
∴MN2=MB2+ND2;
(3)由(1)知,Rt△ABE≌Rt△AGE,Rt△ADF≌Rt△AGF,
∴BE=EG=4,DF=FG=6,则EF=10
设AG=x,则CE=x-4,CF=x-6.
∵CE2+CF2=EF2,
∴(x-4)2+(x-6)2=102.
解这个方程,得x1=12,x2=-2(舍去).
∴AG=12.(9分)
∴BD=
| AB2+AD2 |
| 2AG2 |
| 2 |
在(2)中,MN2=MB2+ND2
设MN=a,则a2=(3
| 2 |
| 2 |
| 2 |
∴a=5
| 2 |
| 2 |
点评:本题考查了正方形的性质、直角三角形的性质、全等三角形的判定和性质以及勾股定理的运用和一元二次方程的运用,题目的综合性很强,难度不小.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
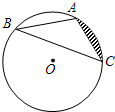 (2012•丰润区二模)如图,已知:△ABC是⊙O的内接三角形,∠B=30°,若AC=6,则图中阴影部分的面积是( )
(2012•丰润区二模)如图,已知:△ABC是⊙O的内接三角形,∠B=30°,若AC=6,则图中阴影部分的面积是( )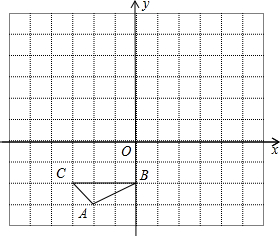 (2012•丰润区二模)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
(2012•丰润区二模)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.