题目内容
15. 如图,在平面直角坐标系xOy中,点A,B在双曲线y=$\frac{k}{x}$(k是常数,且k≠0)上,过点A作AD⊥x轴于点D,过点B作BC⊥y轴于点C,已知点A的坐标为(4,$\frac{3}{2}$),四边形ABCD的面积为4,则点B的坐标为($\frac{8}{3}$,$\frac{9}{4}$).
如图,在平面直角坐标系xOy中,点A,B在双曲线y=$\frac{k}{x}$(k是常数,且k≠0)上,过点A作AD⊥x轴于点D,过点B作BC⊥y轴于点C,已知点A的坐标为(4,$\frac{3}{2}$),四边形ABCD的面积为4,则点B的坐标为($\frac{8}{3}$,$\frac{9}{4}$).
分析 先连接BO、BD,根据点A的坐标求得反比例函数解析式,进而求得△BOC的面积=△BCD的面积=3,再根据四边形ABCD的面积为4,求得△ABD的面积=4-3=1,最后根据AD=$\frac{3}{2}$,求得点B的坐标.
解答 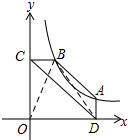 解:连接BO、BD,
解:连接BO、BD,
∵点A在双曲线y=$\frac{k}{x}$(k是常数,且k≠0)上,点A的坐标为(4,$\frac{3}{2}$),
∴k=4×$\frac{3}{2}$=6,
又∵BC⊥y轴于点C,
∴BC∥OD,
∴△BOC的面积=△BCD的面积=3,
又∵四边形ABCD的面积为4,
∴△ABD的面积=4-3=1,
设B(a,$\frac{6}{a}$),
∵AD⊥x轴于点D,A的坐标为(4,$\frac{3}{2}$),
∴AD=$\frac{3}{2}$,
∵$\frac{1}{2}$×$\frac{3}{2}$×(4-a)=1,
解得a=$\frac{8}{3}$,
∴$\frac{6}{a}$=$\frac{9}{4}$,
∴点B的坐标为($\frac{8}{3}$,$\frac{9}{4}$).
故答案为:($\frac{8}{3}$,$\frac{9}{4}$).
点评 本题主要考查了反比例函数系数k的几何意义的运用,解决问题的关键是作辅助线构造三角形,根据三角形的面积求得点B的坐标.解题时注意数形结合思想的运用.

练习册系列答案
相关题目
6.若分式$\frac{x+2}{x-2}$的值为零,则x等于( )
| A. | 0 | B. | 2 | C. | -2 | D. | ±2 |
10.若一次函数y=k1x与反比例函数y=$\frac{{k}_{2}}{x}$的图象没有交点,则k1,k2的值可能是( )
| A. | k1=1,k2=-2 | B. | k1=1,k2=2 | C. | k1=-1,k2=-2 | D. | k1=1,k2=1 |
4.长度为下列数据的各组线段中,能构成一个直角三角形的是( )
| A. | 3,4,8 | B. | 12,13,5 | C. | 5,6,8 | D. | 4,6,11 |
5. 如图,在⊙O中,CD是直径,弦AB⊥CD于E,顺次连接AC,CB,BD,DA,则下列结论中错误的是( )
如图,在⊙O中,CD是直径,弦AB⊥CD于E,顺次连接AC,CB,BD,DA,则下列结论中错误的是( )
 如图,在⊙O中,CD是直径,弦AB⊥CD于E,顺次连接AC,CB,BD,DA,则下列结论中错误的是( )
如图,在⊙O中,CD是直径,弦AB⊥CD于E,顺次连接AC,CB,BD,DA,则下列结论中错误的是( )| A. | $\widehat{AC}=\widehat{BC}$ | B. | AE=EB | C. | CD平分∠ACB | D. | BA平分∠CBD |
 已知有理数a、b、c在数轴上所对应的点如图所示,则$\frac{b+c}{a}$<0.
已知有理数a、b、c在数轴上所对应的点如图所示,则$\frac{b+c}{a}$<0. 如图,一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=-$\frac{8}{x}$的图象在第二象限交于点C,如果点A的坐标为(2,0),B是AC的中点,则该一次函数的解析式是y=-x+2.
如图,一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=-$\frac{8}{x}$的图象在第二象限交于点C,如果点A的坐标为(2,0),B是AC的中点,则该一次函数的解析式是y=-x+2. 如图,四边形OABC是矩形,四边形ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=12,则正方形ADEF的边长为4.
如图,四边形OABC是矩形,四边形ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=12,则正方形ADEF的边长为4.